What is a Radian?
One Radian is defined to be the angle subtended (formed) from the center of a circle which intercepts an arc equal in length to the radius of the circle.
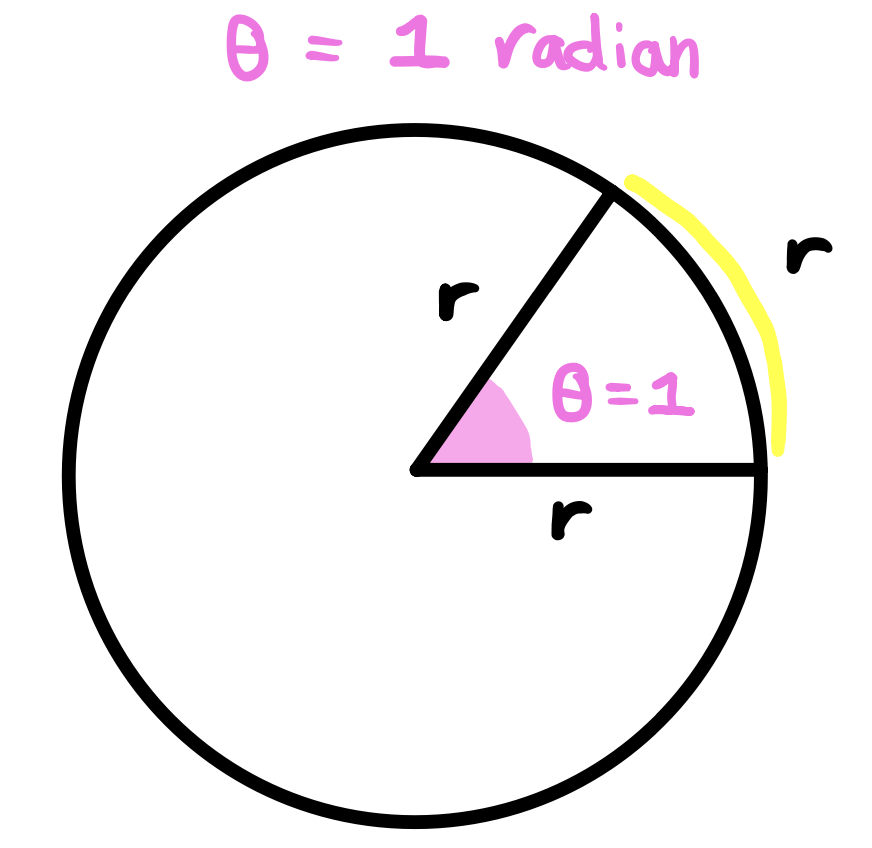
What does this mean? If we have an angle that starts at the center of the circle where the arc formed by the two radii of this angle is also equal to the radius, then the this angle is measured at 1 radian. In the figure above, we see that the radius is \(r\) and the arc length formed by the two radii is also \(r\). Therefore, the angle has a measure of 1 radian. This is true for any circle of any size.
What if the radius is not equal to the arc length?
So now that we defined what a radian is, how can use it to measure a different angle where the arc length is not necessarily equal to the radius of the circle?
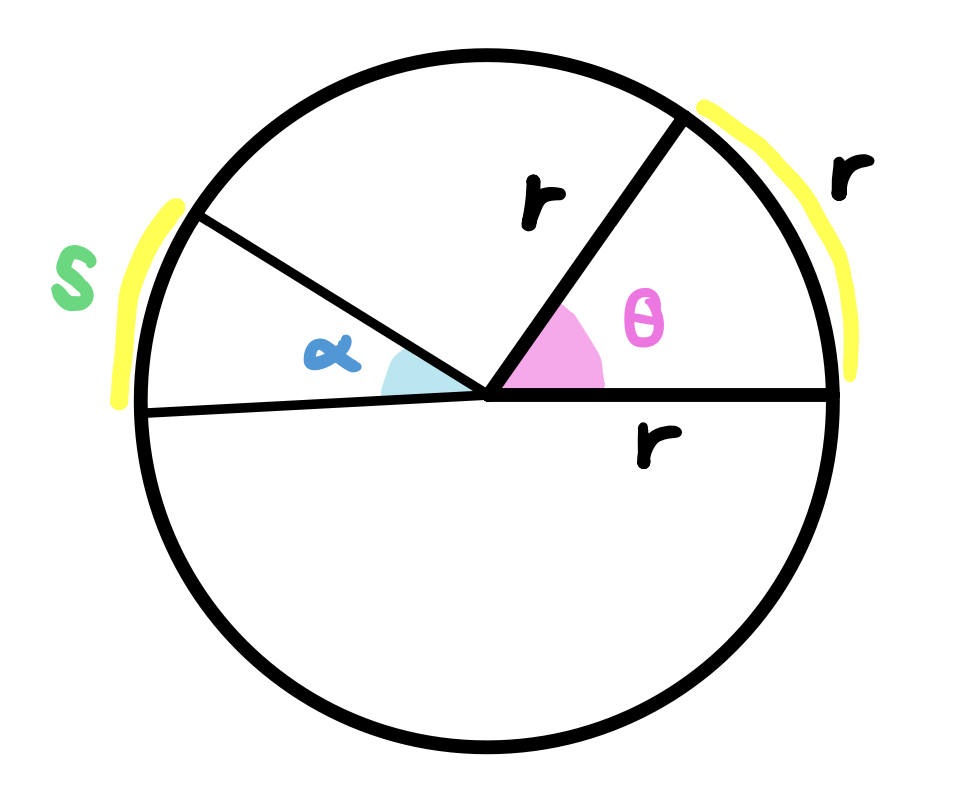
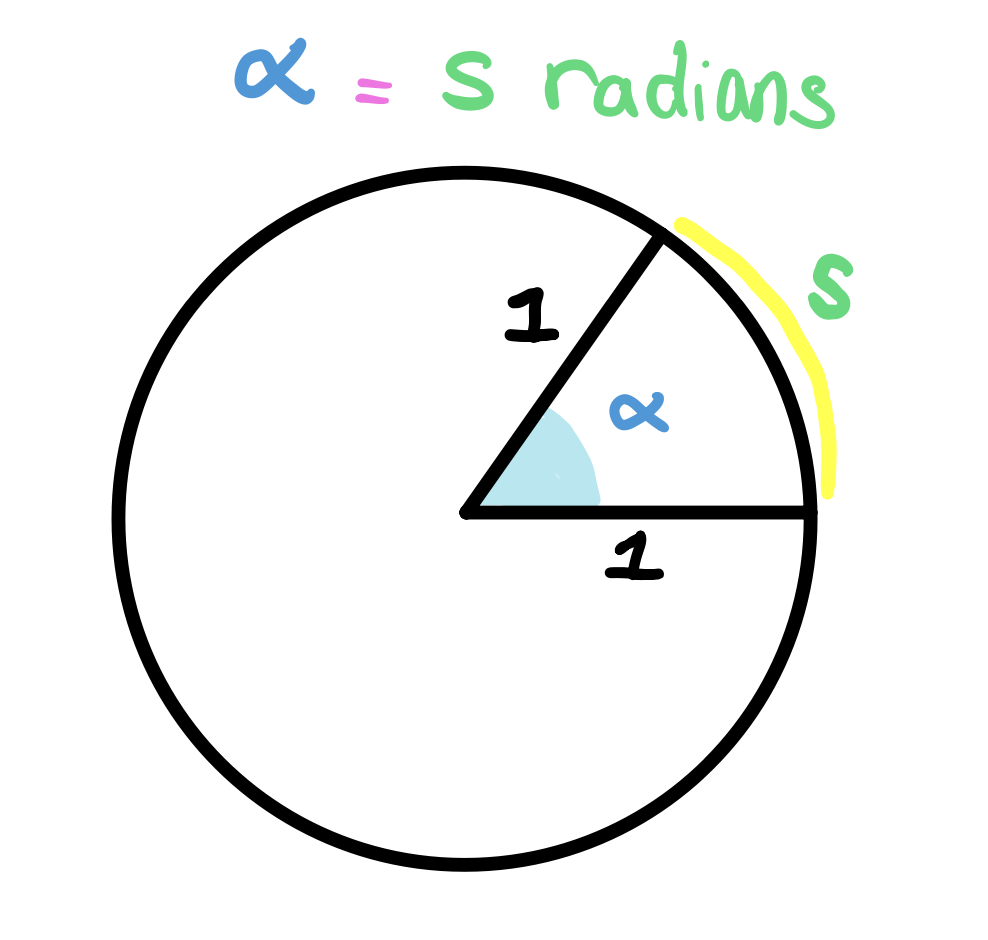
In the figure above, we have another angle \(\alpha\) where the radius and the arc length are not the same. We know (HOW???) that the measures of the central angles of a circle are proportional to the lengths of their arcs. So we can write something like this,
But we know by definition that \(\theta\) is exactly 1 radian. This is how we defined the radian to be. So,
In other words, The angle \(\alpha\) is the ratio of the arc length \(s\) divided by the radius. And this is again true for any circle of any size. It is a formula that we’ve seen in a lot of times over and over again.
The Unit Circle
The unit circle is a special case because the radius is 1. This makes any angle alpha directly equal to the arc length!
How many radians in one revolution around the circle?
The ratio of the circumference (\(c\)) to the diameter (\(d\)) of the circle (any circle) is the constant \(\pi\).
This means that the circumference is given by,
What we want to know is how many arc lengths of length \(r\) are there in the circumference that has length \(2\pi r\)?
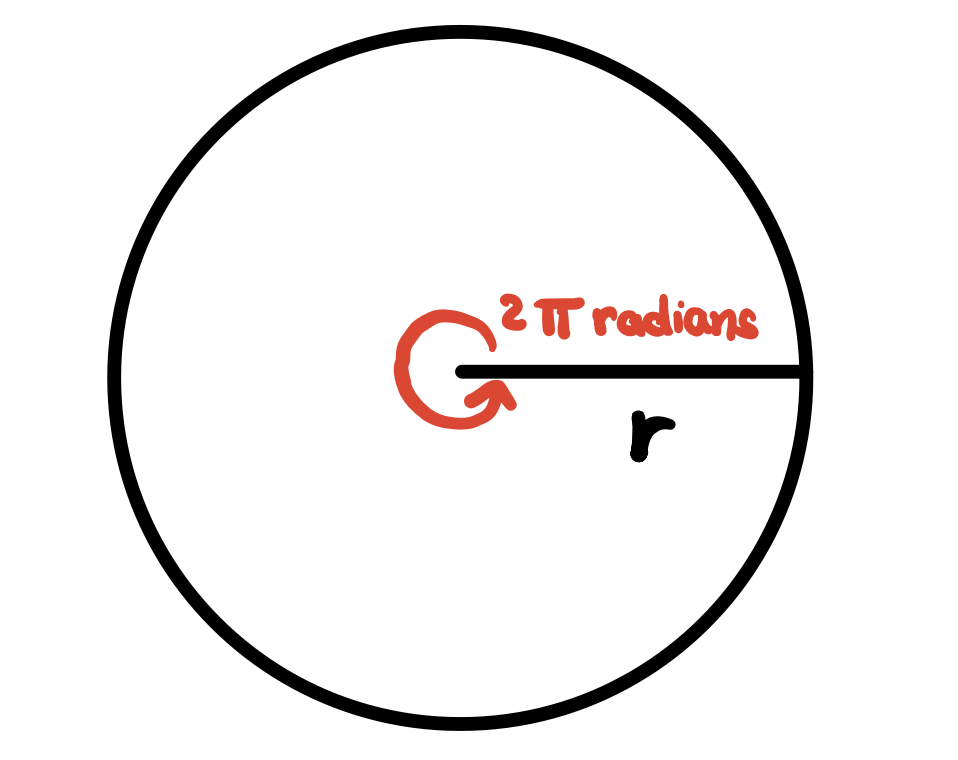
This means if we take the circumference and divide it into pieces where each piece is of length \(r\), we’ll have a total of \(2\pi\) arcs. \(2\pi\) is about 6.28. So 6.28 of arc lengths of length \(r\)! See below,
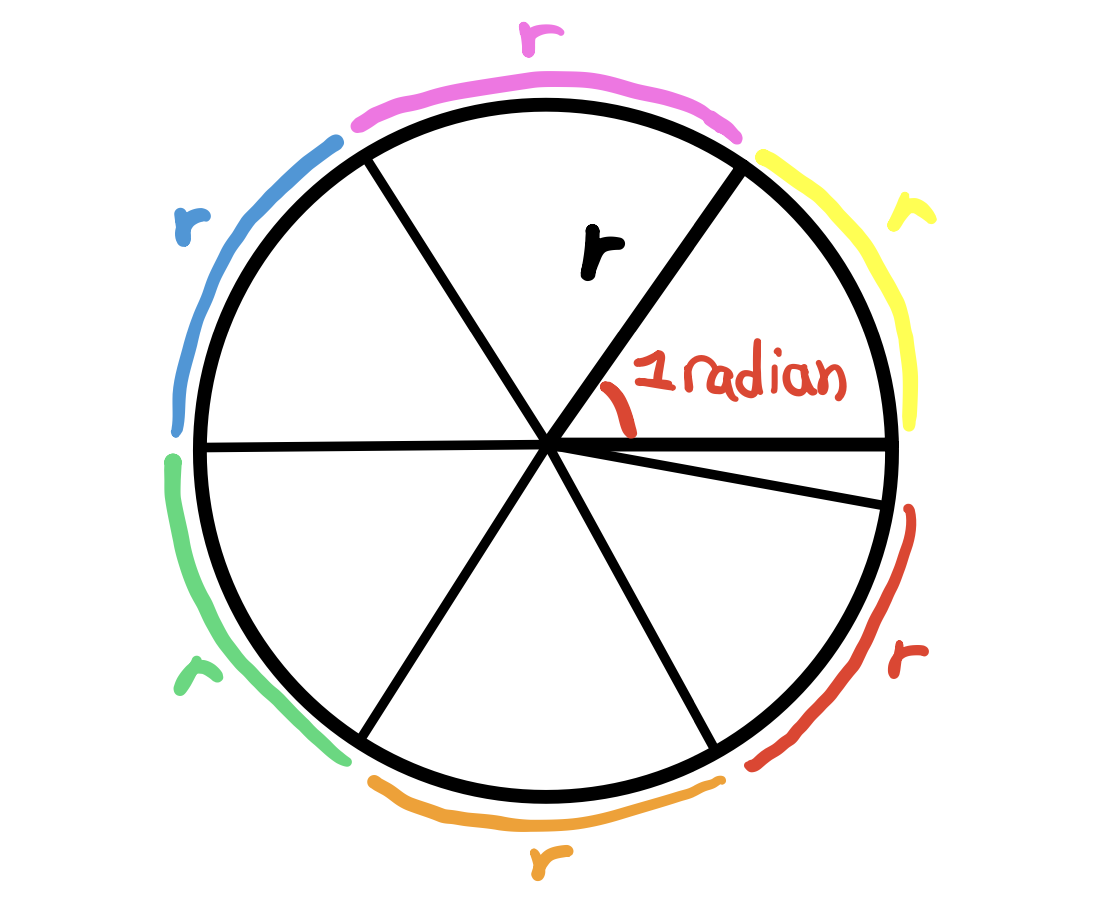
Now, we know that the radian was defined to be 1 for the center angle that intercepts an arc of length equal to the radius. This is defined already. This means that each of these arcs correspond to an angle measured at 1 radian exactly. This implies that to go a whole rotation around the entire circle we need \(2\pi * 1 = 2\pi\) radians!
Radians and Degrees
What is the relationship between degrees and radians? We know a whole rotation around the circle is exactly 360 degrees. Therefore 360 is equivalent to \(2\pi\) or in other words, 1 radian is equal to 57.2958 degrees and that’s where the conversion formula between degrees and radians come from!