Note

These are my rough notes based on attending CS148. They might contain errors so proceed with caution!

Introduction

What is Light? Light consists of photos that travel along straight paths until they hit a surface. Photons carry some energy represented by its wavelength. A large amount of photons of different energies will together represent a spectrum. The sun emits electromagnetic radiation across a wide spectrum of wavelengths that includes both visible and not-visible light to the human eye. This includes radio waves, microwaves, visible light, ultraviolet etc. These forms of radiation differ in their wavelengths and frequencies. When lights hits an object, this light is either

  • Absorbed: This means that the object just absorbed and transformed these photons into some other energy (maybe heat for example). We don’t care about these photos because they’re not visible to us.
  • Reflected: The light that didn’t get absorbed can be reflected. This light then will hit our eyes and we then will perceive color. For example, If the car is red, this means a lot of the red photons are bouncing off and all the other photons are being absorbed.

Light can also pass through the material (maybe the object is made of glass) and can get bent, scattered and so on. When the light hits the eyes, the brain will create a signal and send it to the brain. The brain then will create an image based on these signals. So color doesn’t really exist. It’s just the brain’s interpretation of the signal generated after the photos reached the back of our eyes.

Physics of Light

The visible spectrum of the full electromagnetic spectrum of light is really tiny (refer to the slides), but that’s all our eyes care about. Either the wavelengths or the frequencies are usually used to differentiate them but in Graphics, we mostly care about wavelengths.

Light carries multiple wavelengths. How did we figure out the wavelength that makes us see red? From experiments, we’ve combined different colored lights and observed the results. This led to discovering the relative power distributions (TODO: add figure).

What happens if we shine a red colored light and another green colored light? We will see that the energy adds up. In fact, we’ll have the figure on the right where the peak is now is at 600 instead (yellow light). These two green and red distributions are added together ($E = E_1(\lambda) + E_2(\lambda)$). What if we shine green, red and blue light? We get white light!

What happens if we add red, blue and green paint together? do we get white paint? no! we see black/brown paint. This is because we’re now subtracting light. Why is that? How come

Additive vs. Subtractive Color Spaces

So why is paint subtractive? why didn’t we add the energies up like when we shined multiple light sources together? With paint, the pigments in the paint absorb certain wavelengths of light. These absorbed wavelengths are then subtracted from the incoming light.

Where do we find additive color spaces? Displays are one major example. The monitor uses three color lights that get shined into our eyes. It is additive. Suppose that we’ve shine a light source on multiple surfaces:

  • If the surface is red, then it's going to absorb all the light except for red which will bounce.
  • If the surface is white, then white (all three) is going to bounce
  • If the surface is black, then all light will be absorbed and nothing is bounced.

In general, we absorb the stuff that we don’t reflect. So the color something is what’s being reflected and everything else is being absorbed. We can actually plot this reflected light energy.

$$ \begin{align*} $Reflected(\lambda)=E(\lambda)r(\lambda) = E(\lambda)(1-a(\lambda))$. \end{align*} $$

where $r(\lambda)+a(\lambda)=1$ (light is either reflected or absorbed!). This means is that you can’t know what color an object is. By creating a color for the object, you have to know what kind of light you’re shining on it.

Sensor Absorption (How does the eye take in the light?)

The sensor (whether a sensor or the eye) absorbs the light coming in (per unit time) and creates a signal (per unit time). This amount of current that we generate is all we know and nothing else. The cones in our eyes work the same way. To compute the signal power (energy per power), we need to take the integral over $a(\lambda)$ which is the absorption.

$$ \begin{align*} A = \int E(\lambda)a(\lambda)d\lambda \end{align*} $$

Again, this light comes in to our eyes. We know all these wavelengths and their frequencies. We then want to sum all the wavelengths of the energy coming in. Specifically we want to sum only the portion of it that is getting absorbed by our eyes. $A$ is the total energy that the sensor picked up from the light which is going to be used to generate the current.

Human Eye

The human eye has 3 types of cones sensors and 1 type of rod sensors. Proteins in the cone/rods absorb the incoming photons changing the cell’s membrane potenial, thus creating a signal that gets interpreted by the brain. The cones are more optimized for seeing during the day while the rods’ signals are over-saturated. During the night, the rods are more optimized for seeing and the cones’ signals are under-saturated. For the rods for example, seeing during the day is like as if we stared directly into the sun! they’re not optimized for sunlight!

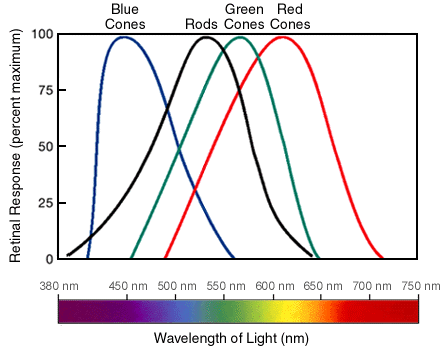
Each cone and rod cell has a specific absorption (response) function. This absorption function gives is what tells us how good a certain cell at absorbing certain wavelengths. As we’ve expected, one of the cones is really good at the “red” wavelength, one is good at “blue” and the last is good at “green”. The rod cell is really good at green. This is one reason why humans really good at seeing green.

Let’s look at an example. Suppose we shine a light that has a single emission of a specific wavelength that is equal to 520. We then shine this light at a human eye. What will happen? The red cone will absorb very little of the light (let it be A). The green blue cone, a little more. Let that amount be B. Finally, the green cone absorbs of it (let it be C). So, since C is the biggest number, then the brain will see green! but wait, light coming into our eyes is not coming as a single wavelength. It comes with different wavelengths and frequencies. So how does the eye interpret all of us? We’ll integrate over the absorption function for each cell and get the three numbers $A$, $B$ and $C$.

$$ \begin{align*} A = \int E(\lambda)a(\lambda)d\lambda \end{align*} $$


The Trichromatic Theory

The previous example implies that we really only need 3 “colors” to re-create/trick the brain into seeing the same color again and this is exactly what scientists did. The idea is that if you have three lasers (single emission of a specific wavelength eg R=700, G=546 and B=436). Then a human is given an object with a “color”. We’ll then use the laser combinations to match that same exact “color” and the human mistakenly believes it’s the same color! This works again because each of the three cones can only send one signal (so 3 dimensional basis). This is why we only use red, green and blue lights in our computers, printers etc. So for example, based on the trichromatic theory, each pixel in an image will only need three numbers!


3D Color Spaces

Since we only need three colors, we can just work in three dimensions and we don’t need the entire spectrum. So we have this huge amount of light hitting the camera but once it hits the camera, the camera is going to have three cones and will knock this light down to only three values. So simple.

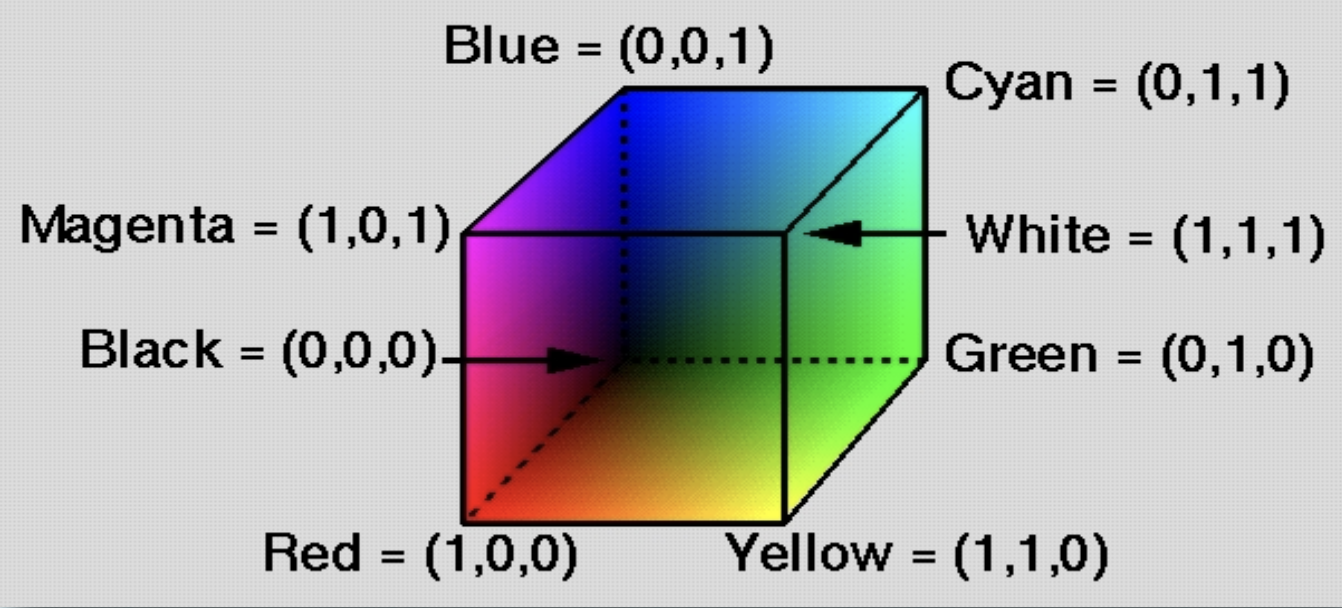
To construct this three dimensional space of colors, map each primary color (red, green, blue) to the unit distance along the \(x,y\) and \(z\) axes. Black is at \((0,0,0)\) and White is at \((1,1,1)\). The resulting RGB cube represents all possible color.

Another color space that can be constructed is the The cylindrical HSV color space. This is a color space based on hue, saturation and value. saturation is the intensity for a partical color. value is lightness or darkness of a particular color.

Another color space is the Luminance and Chrominance (YUV). This color space was used back in black and white television sets. Why? Because the “Y” component holds most of the spatial details of the image. Therefore, we can aggressively compress the other components $U$ and $V$ since we don’t care about color and still maintain a good quality.

Mapping between Color Spaces

To go back and forth between these color spaces is easy! we just need to find the transformation to take us from one to the other since we’re all working in $R^3$. One can map from YUV to RGB using the following matrix (TODO: ADD THE MATRIX from the Slides). Notice in the matrix that 0.58 percent of Y is coming from the green channel. This emphasizes the point that if you want to see more detail then you want to emphasize the green light. Does this mean that we need to change important signs to be colored green because it contains more details? No…. it doesn’t matter what the eyes see. After all it’s a signal that is sent to the brain. What matters is what the brain does with the signal. The brain reacts faster to red for example than yellow or green.

Spatial Resolution

The cones in the eyes have resolution as well. TODO …

References

Fundamentals of Computer Graphics, 4th Edition
CS148 Lectures