Introduction
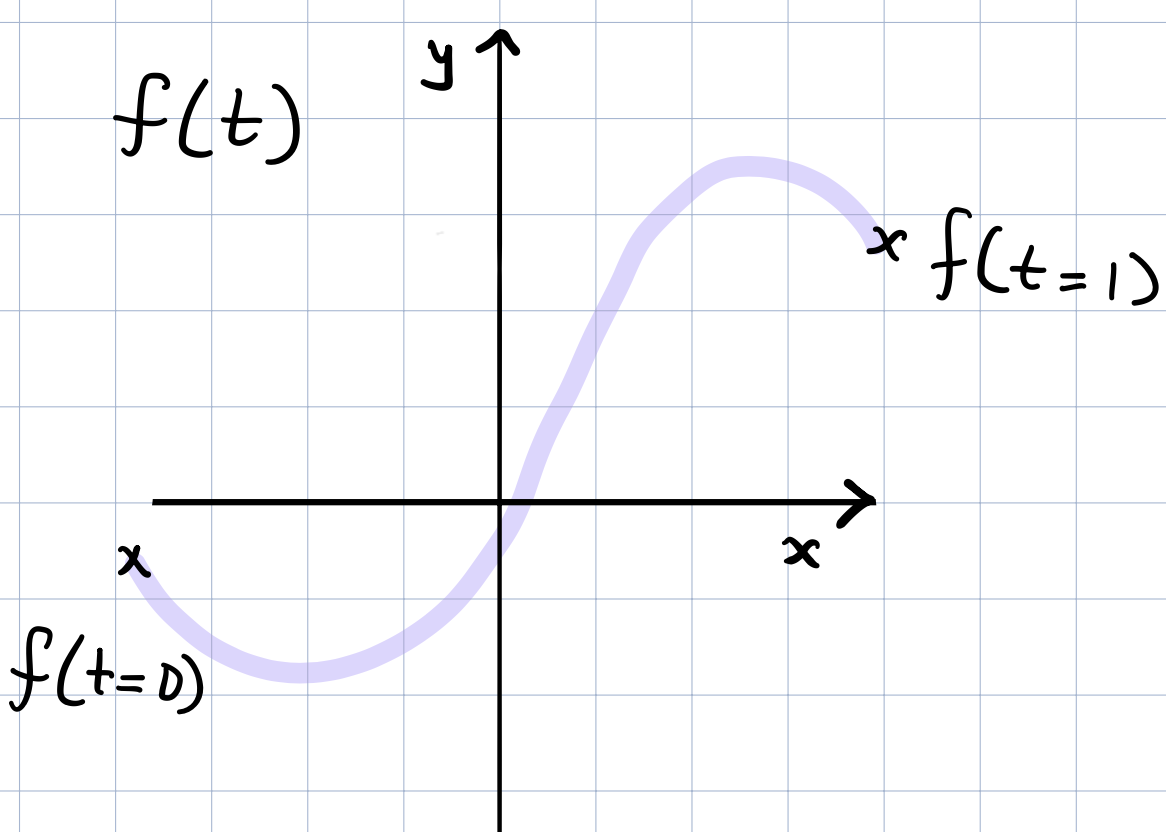
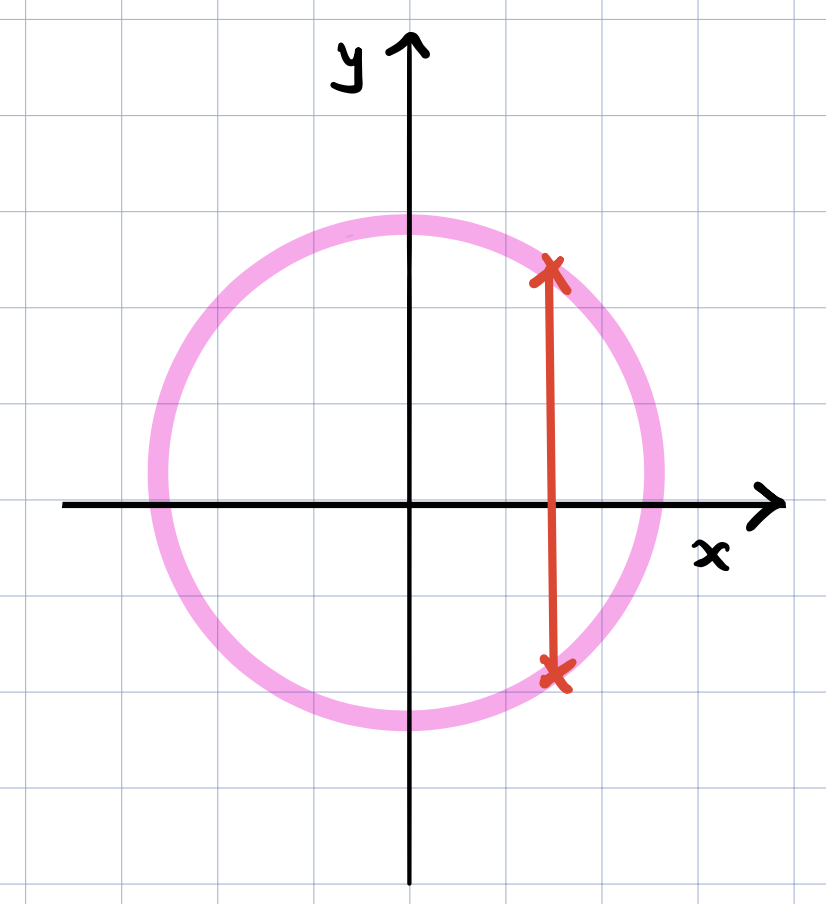
We’ve already seen the implicit representation in the previous post. This time, we will focus on the parametric representation. The parametric representation describes the line or curve using one or more new variables. This variable is commonly denoted as “t”. For example, we might want to describe a curve with a specific start point, an end point and furthermore we might a want a general independent parameter that once we specify, then we get back a point \((x,y)\) on the curve. More importantly, some curves can be represented with the explicit representations because we can’t describe \(y\) as a function of \(x\)! See this for example. \(x=1.5\) has two possible \(y\) values!
Example
Suppose we’re given this line in its implicit form,
The parametric representation will be the following
It will be clear later on how we derived these terms but for now let’s make sure that we can substitute multiple values of \(t\) to see that these points are indeed on the line. You can try \(t=0\) to get \((x=0, y=1)\) and see that it indeed satisfies the implicit equation. But now ended up with two functions. Is there a way to simplify this? Yes, we can wrap everything in one function if we used vectors instead! So let \(v = [x, y]\) be a vector and then re-write the previous two equations such that
It looks really good but how do we derive these constants? This part is pretty cool. Take two points on the line. For example \(p_0=(0,1)\) and \(p_1=(2,2)\). and now we can see that we can represent this line as with the initial point \(p_0\) and then the direction of the line using \(p_1-p_0\) so,
At \(t=0\), we’re at \(p_0\). If we’re at \(t=1\), we’re at \(p_1\). And we can still substitute \(t\) values to go beyond this range. We can also re-write this to clean it and replace \(v\) with \(f(t)\) since this is now just a function of \(t\),
But there is one more way to write this! re-arrange the terms such that,
So really, it’s like we’re interpolating between the two points. This notation is also nicer since the two points appear once each!