The Implicit Representation

In the implicit form of representing some geometry we specify the relationship between the points such that for some point \((x,y)\), if \(f(x,y)=0\), then this point is on our shape (line, circle, etc). This makes it easy to describe shapes. We can get a pretty compact form. It also makes it super easy to check whether a point belong to our shape or if it doesn’t. Other queries like distance to the surface can also be easy. The downside of this is that we don’t have a way to list all the points directly that satisfy our shape (Explicit Representation) and it’s very difficult to describe complex shapes with implicit representations.



The implicit Representation of a Line

Consider the following equation for a line that goes through the origin,

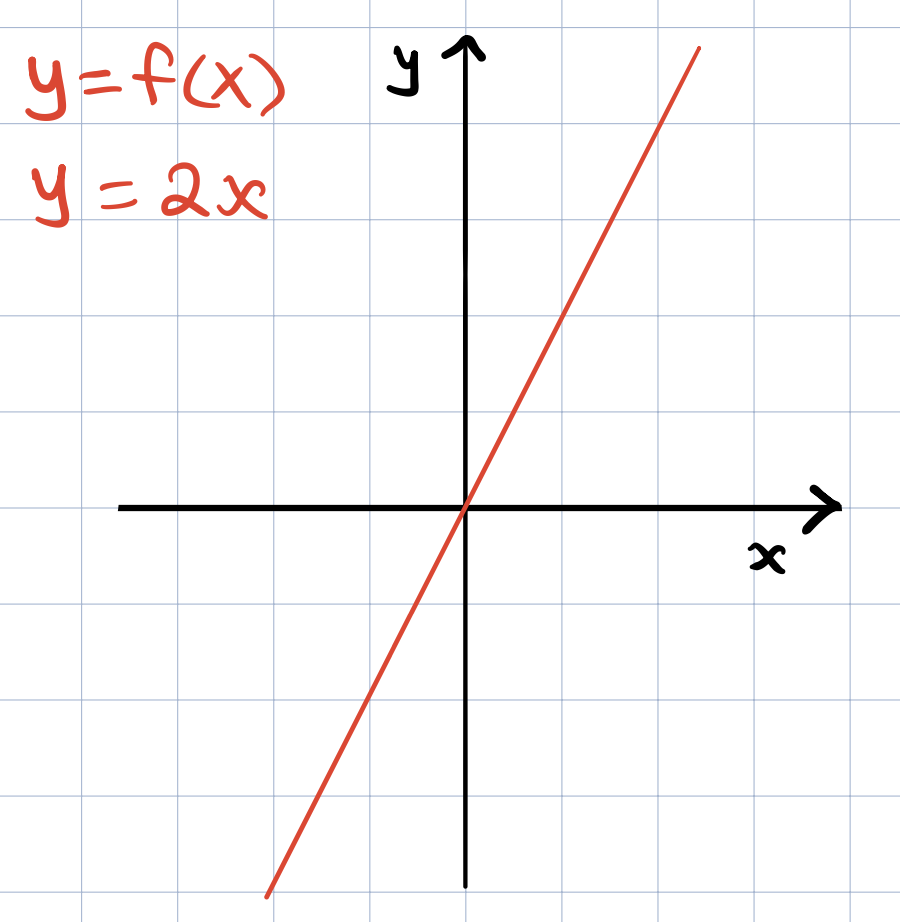
This line equation (\(y = 2x\)) is also sometimes referred to as the explicit representation of the line. We can also represent this line using a representation called the implicit representation. We can do so by re-arranging the terms such that

$$ \begin{align*} y - 2x = 0. \end{align*} $$

The implicit representation describes the relationship between the variables \(x\) and \(y\). It describes all the points \((x,y)\) that satisfies the equation \(y - 2x = 0\). We just know the relationship between the variables that will need to be satisfied. In general, the implicit representation of a line takes the form

$$ \begin{align*} f(x, y) &= 0 \\ ax + by + c &= 0. \end{align*} $$

We don’t know the points directly. We just know that the points satisfy some relationship such that \(f(x,y)=0\).

The implicit Representation of a Circle

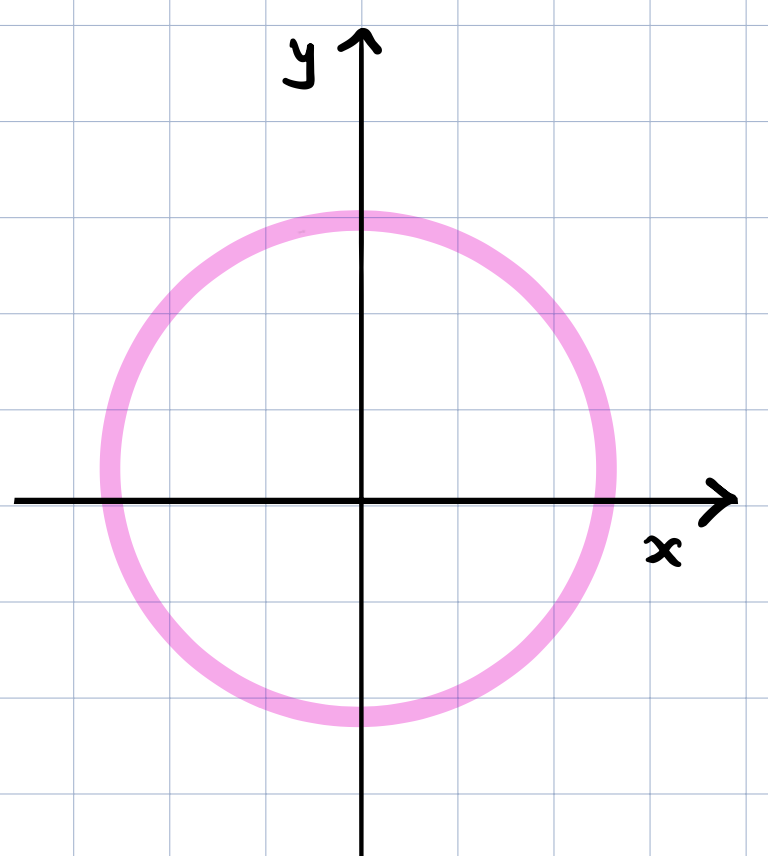
Another example is the equation of a circle. We define a circle by all the points \((x,y)\) such that \(f(x,y) = 0\). If \(f(x,y)\neq 0\), then it’s not on the circle. The equation of a circle can be written as

$$ \begin{align*} f(x,y) &= (x - x_c)^2 + (y - y_c)^2 - r^2 = 0. \end{align*} $$

where \((x_c, y_c)\) is a point and \(r\) is a nonzero real number. Any point that satisfies this equation is on the circle of center \((x_c, y_c)\) and radius \(r\). We can re-write the equation using vectors to simplify the notation. if we let \(c=(x_c, y_c)\) and \(p=(x,y)\), then

$$ \begin{align*} f(x,y) = (p - c) \cdot (p - c) - r^2 = 0. \end{align*} $$

We know that \((p - c) \cdot (p - c)\) is just the length of this vector squared and so

$$ \begin{align*} f(x,y) = \left\lVert p - c \right\rVert^2 - r^2 = 0. \end{align*} $$

This just means that the points \(p\) on the circle are those with a distance \(r\) from the center of the circle at \(c\).

Other Implicit Forms

There are many other implicit representations in graphics. Algebraic Surfaces, Constructive Solid Geometry, Level Set Methods, Blobby Surfaces, Fractals and more.

References