These are notes I took while watching the series The Essence of Linear Algebra by 3Blue1Brown.
Vector Coordinates
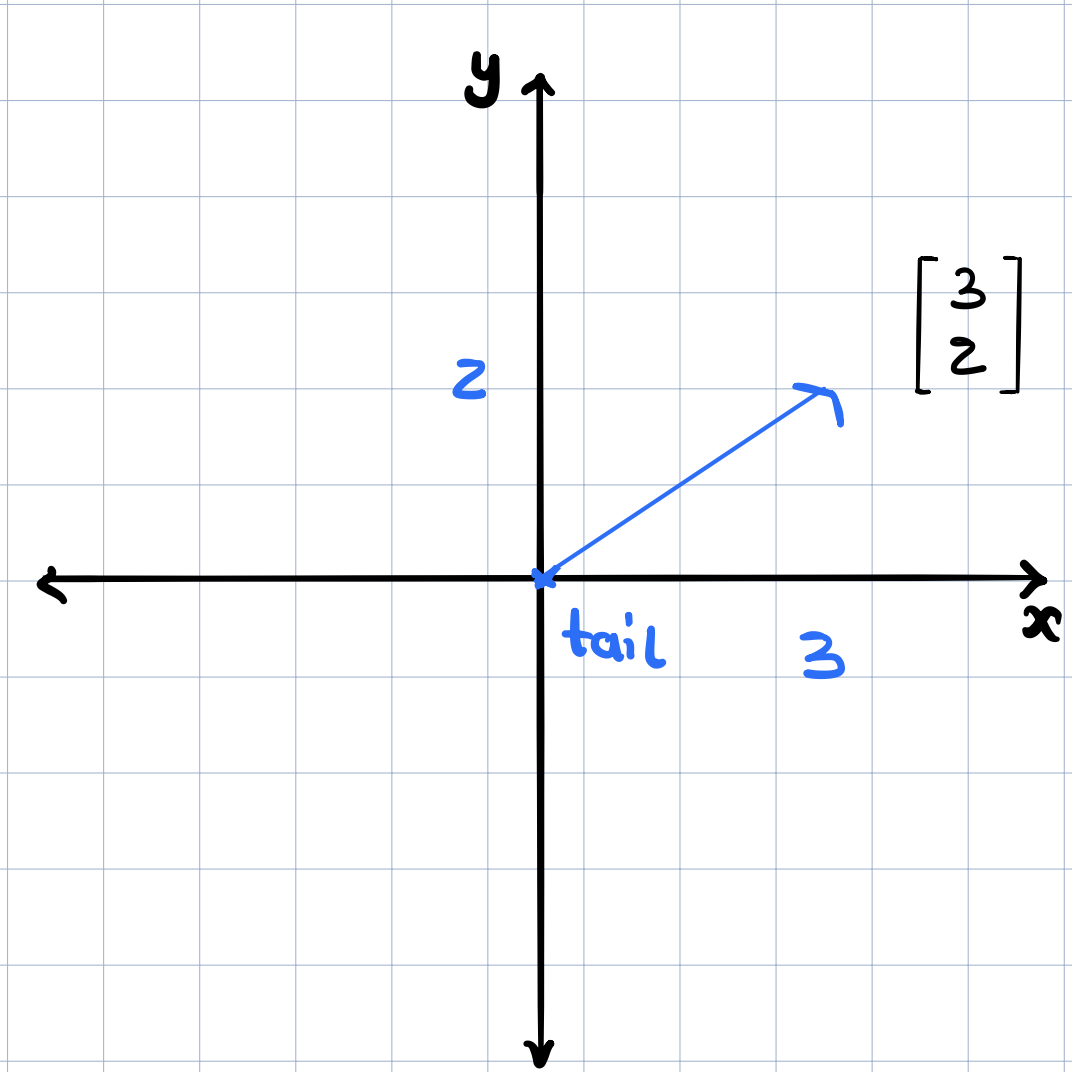
We studied vectors in the previous post and learned about vectors and vector coordinates. The x-coordinate represented the movement from this vector’s tail at the origin along the x-axis to its tip and the y-coordinate represented the movement of this vector along the y-axis. We saw how addition and multiplication were defined and what they meant. This time, we want to think about these vector coordinates differently.
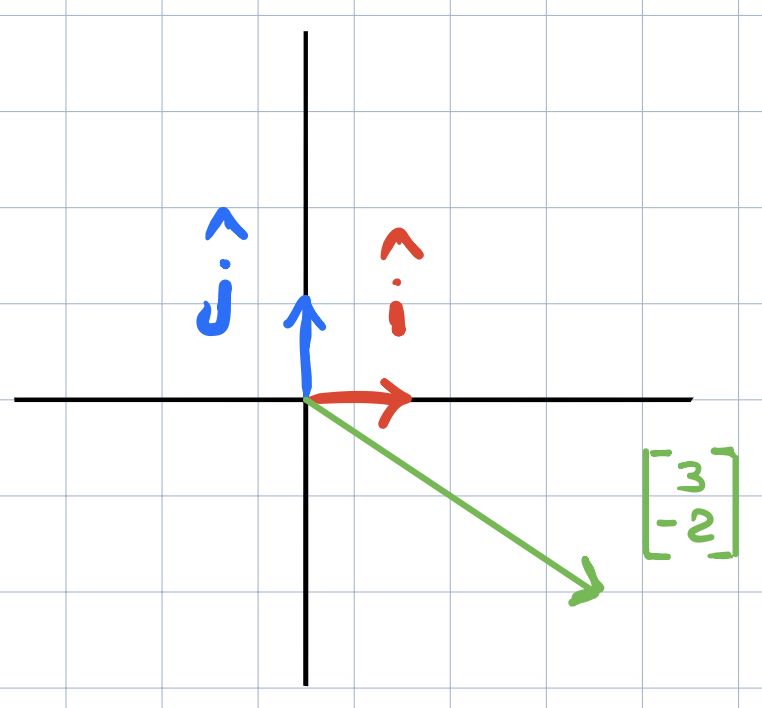
In the xy-coordinate system, we have two special vectors. \(\widehat{i}\) which is a unit vector pointing to the right in the x-direction. \(\widehat{j}\) is a unit vector pointing straight up in the y-direction. Now, given a vector’s coordinate (green vector in the figure above), we will think of each coordinate as a scalar where the x-coordinate scales \(\widehat{i}\) streching it by 3 and the y-coordinate scales \(\widehat{j}\) by a factor of 2 and also flipping it in the other direction. \(\widehat{i}\) and \(\widehat{j}\) are called the basis vectors of the \(xy\) coordinate system. So when we think about coordinates as scalars, these scalars scale the basis vectors.
Linear Combination
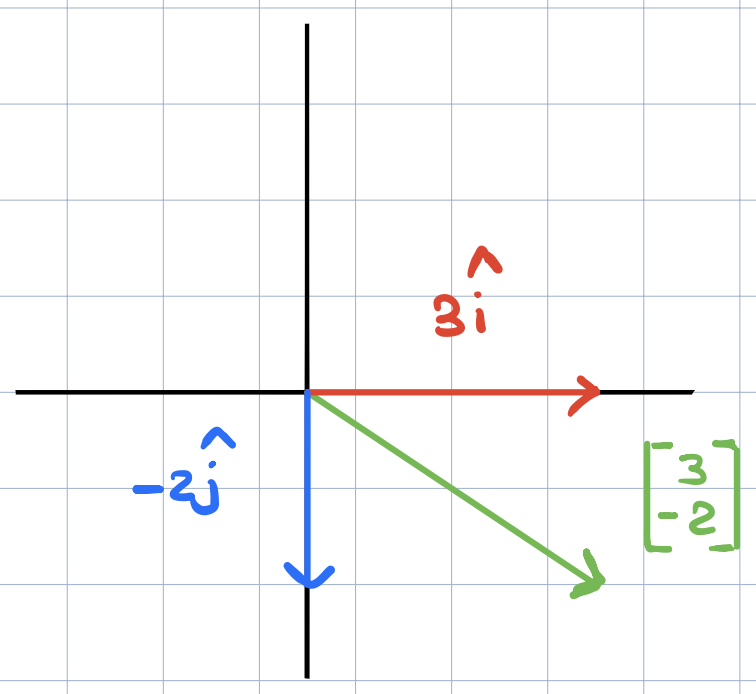
So here the important observation, this means that the vectors that these coordinates describe is really the sum of two scaled vectors \(3\widehat{i} + (-2)\widehat{j}\). (Addition of two scaled vectors!). This sum is also called a linear combination of \(\widehat{i}\) and \(\widehat{j}\). Why did we call it linear? This is really interesting. Grant said to imagine fixing one of the scalars, then changing the other scalar will result in the tip of the resulting vector drawing a straight line. The animation in the video is so great at showing this.
Span of Vectors
Now, if we change both scalars at the same time, then the resulting set is the set of all possible linear combinations of these two vectors and it is formally called the span of these vectors. Moreover, we’ll have three possible sets:
- For most pairs of vectors, we'll reach every possible vector in the plane so their span will be the all vectors of the 2D space
- For the case when both vectors line up, then the tip of the resulting vector is limited to just this single line passing through the origin. So their span is the set of all vectors whose tip sit on that line.
- Both vectors are the zero vector and in this case, we'll be stuck at the origin. So their span is just the zero vector
Vectors vs. Points
Grant said that it gets too crowded thinking about a collection of vectors sitting on a line or all vectors in a plane. So it is common to think of each of these vectors as a point that sits exactly at the tip of each vector where it’s tail is at the origin. So for example previously, we said that the span of two vectors that sit line up is the set of all vectors whose tip sit on that line. But now with the point notation, we can just think of the line itself. In general, it is easier to refer to a collection of vectors by the points that sit at their tips and just think of these points.
Span of Two Vectors in 3D Space
What does the span of two 3d vectors look like? It is a plane cutting through the origin as you would expect. Their span is the set of all possible vectors whose tip sit on that plane. And what happens if we add a third vector? Then we’re back to having three possibilites, the span can be the whole 3D space. If two of the vectors are linearly dependent, then the span is a plane. If all three vectors sit on each other so all of them are linearly dependent, then their span is the line that goes through the origin.
Linear Independence
Formally when two vectors in 2D space sit on top of each other and their span isn’t the whole 2D space, these vectors are called linearly dependent vectors, meaning that one vector can expressed as a linear combination of the other vector. On the other hand, if each vector adds another dimension to the span, then they’re called linearly independent
Basis of a Vector Space
Also formally, the basis of a vector space is a set of linearly independent vectors that span the full space.