These are notes I took while watching the series The Essence of Linear Algebra by 3Blue1Brown.
What are Vectors?
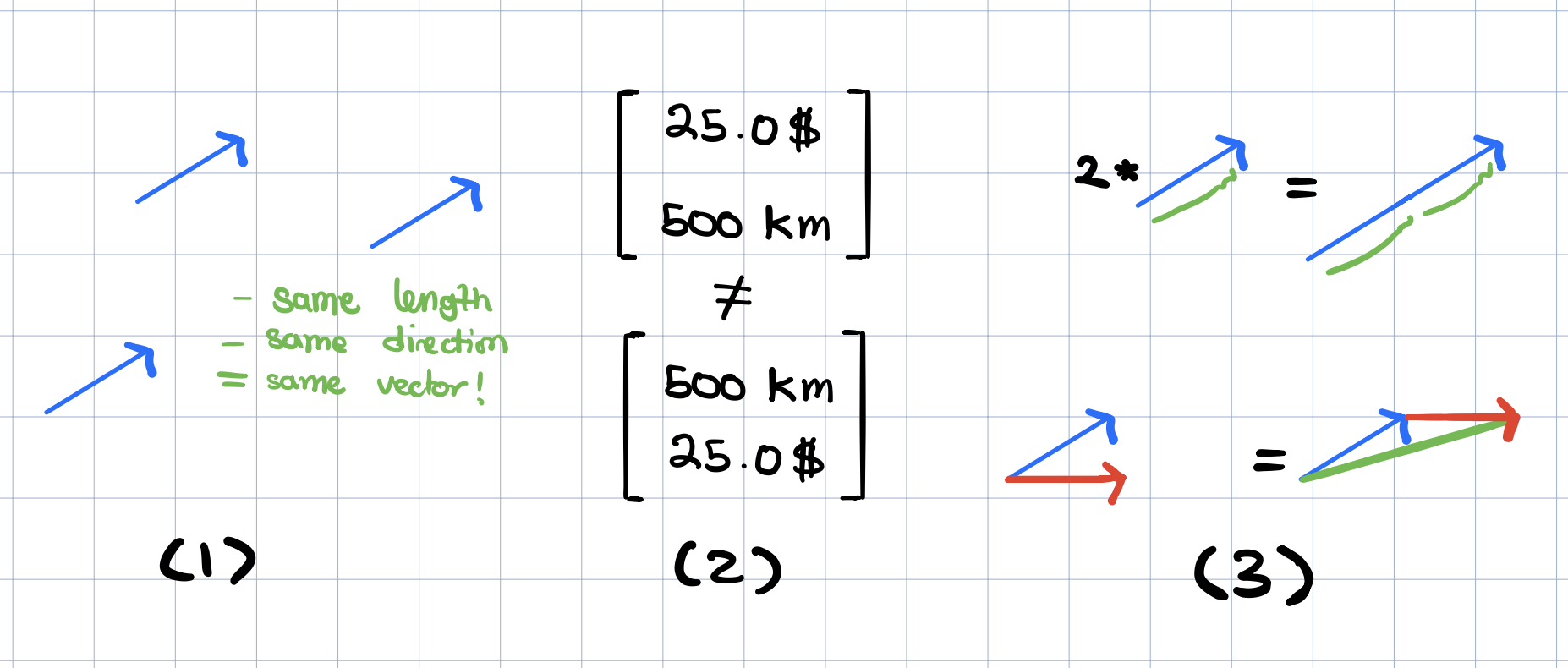
So what are vectors exactly? To a physics student, it is an arrow pointing in space that has a given length and a direction. A vector with a given length and a direction remains the same vector even when moved freely in the space. For a computer science student, a vector is an ordered list of numbers. The vector can be a list of features, a house’s properties, for example. The order matters and so in figure (2), the two vectors are not equal. To a mathematics student, a vector is a more abstract concept. A vector can be anything as long as the operations addition and multiplication are defined.
From Physics to Computer Science
Let’s take the physics student’s idea of a vector being an arrow with a given length and a direction but instead of having it move freely in space, we’ll think of this arrow in a coordinate system with its tail at the origin. See below.
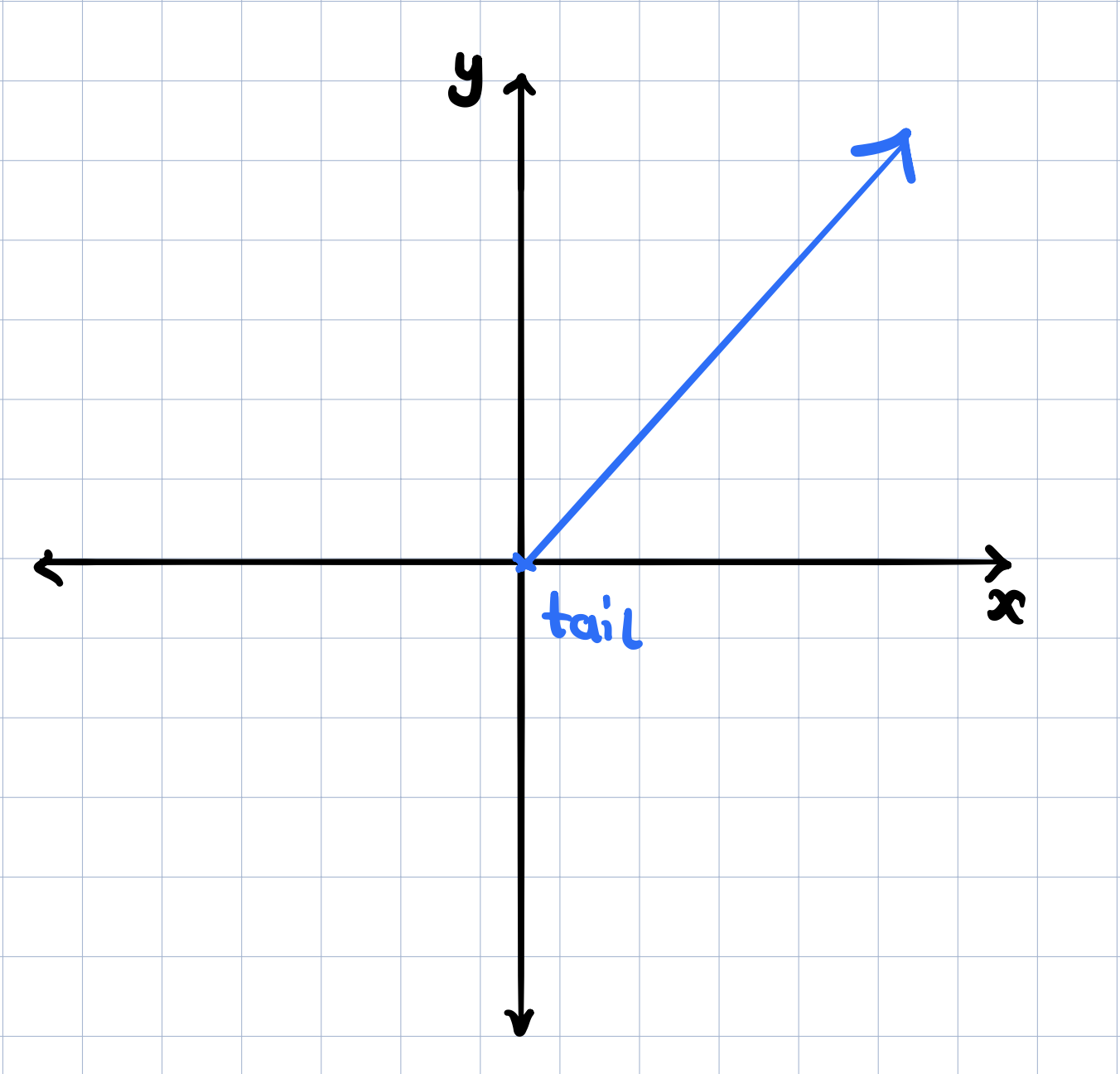
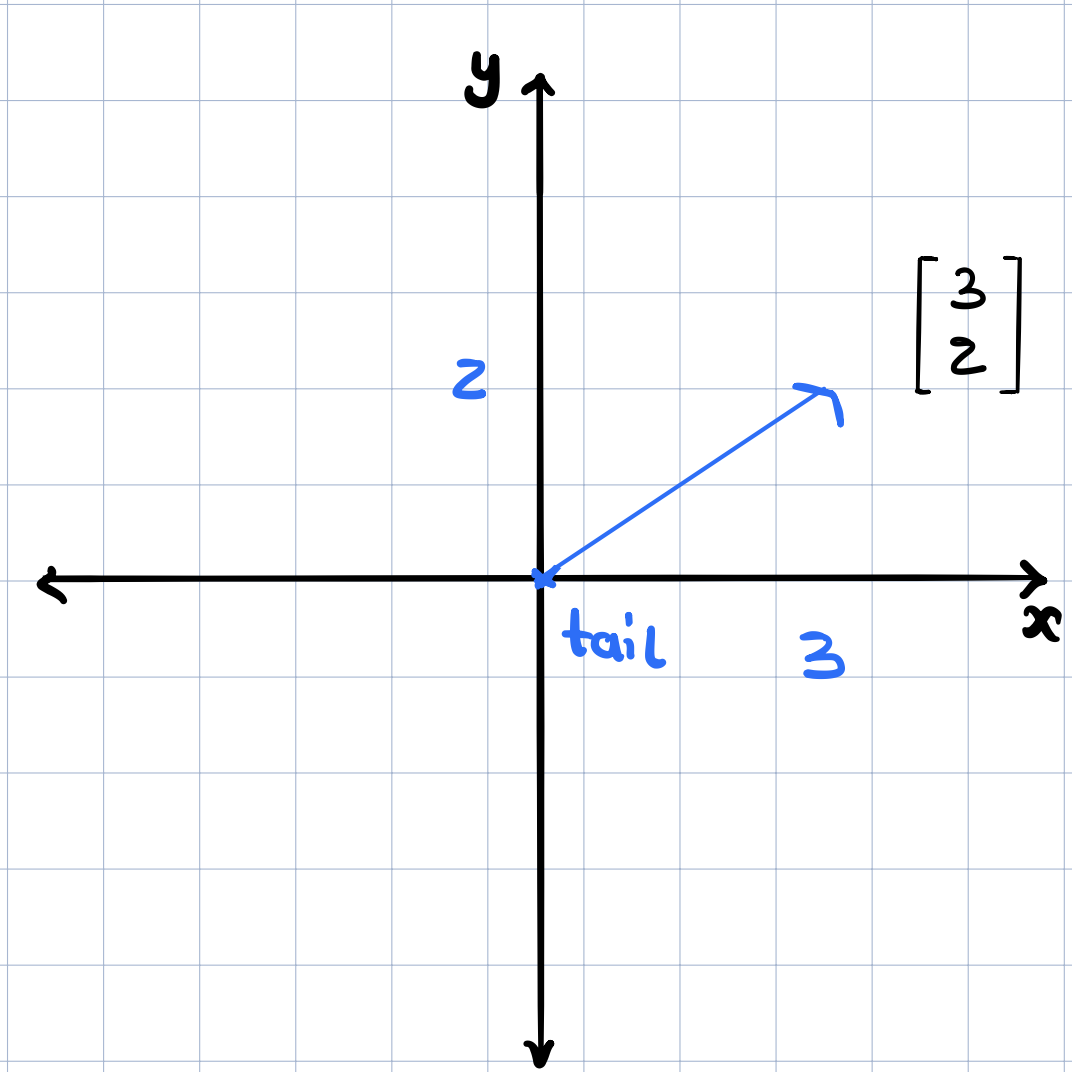
Now that we have the arrow at the origin, we can translate it over to the list of numbers (computer science student’s) point of view by considering taking into account the coordinates of the vector in the coordinate system. What do these coordinates represent? They represent how we can move from the tail of the vector sitting on the origin to its tip. In the example below, 3 tells us how far to walk along the x-axis with positive numbers indicating rightward motion and negative numbers indicate leftward motion. Similarly, 2 tells us how far to walk along the y-axis with positive numbers indicating upward motion and negative numbers indicating downward motion.
From Computer Science to Mathematics
Now that we’ve connected the physics student’s perspective to the computer science student’s predictive. Let’s connect what we’ve developed to the mathematics student’s perspective. Let’s define the two required operations addition and multiplication. Let’s start with addition.
Addition
Suppose we have the following two vectors. To add these two vectors, we will move the second vector so that its tail sits at the tip of the first vector.
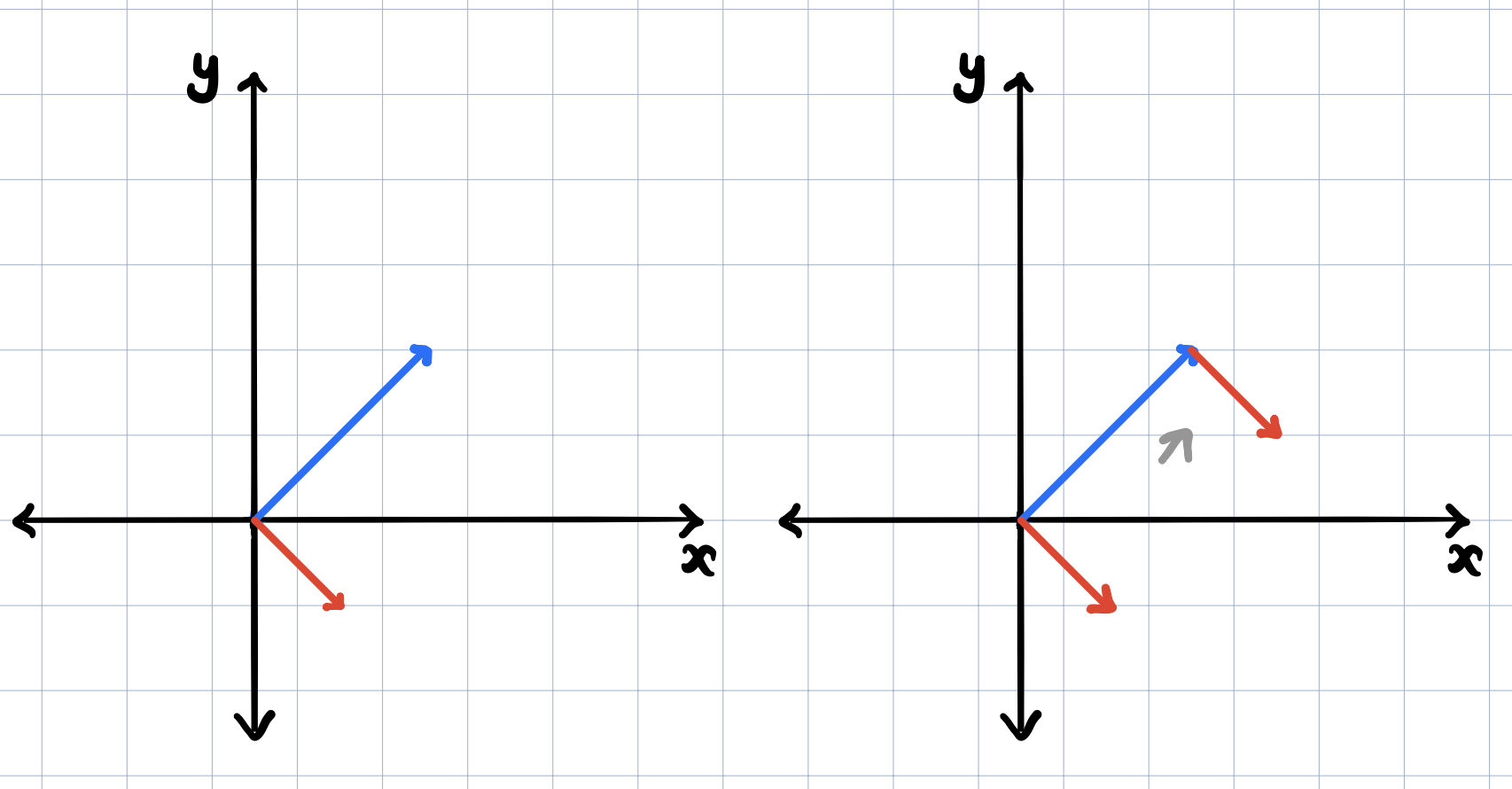
After we do that, now we can draw a vector from the tail of the first vector to the tip of the second vector. This new green vector is the sum of the two vectors. (This is the only time in Linear Algebra where we’re moving a vector away from the origin! interesting!)
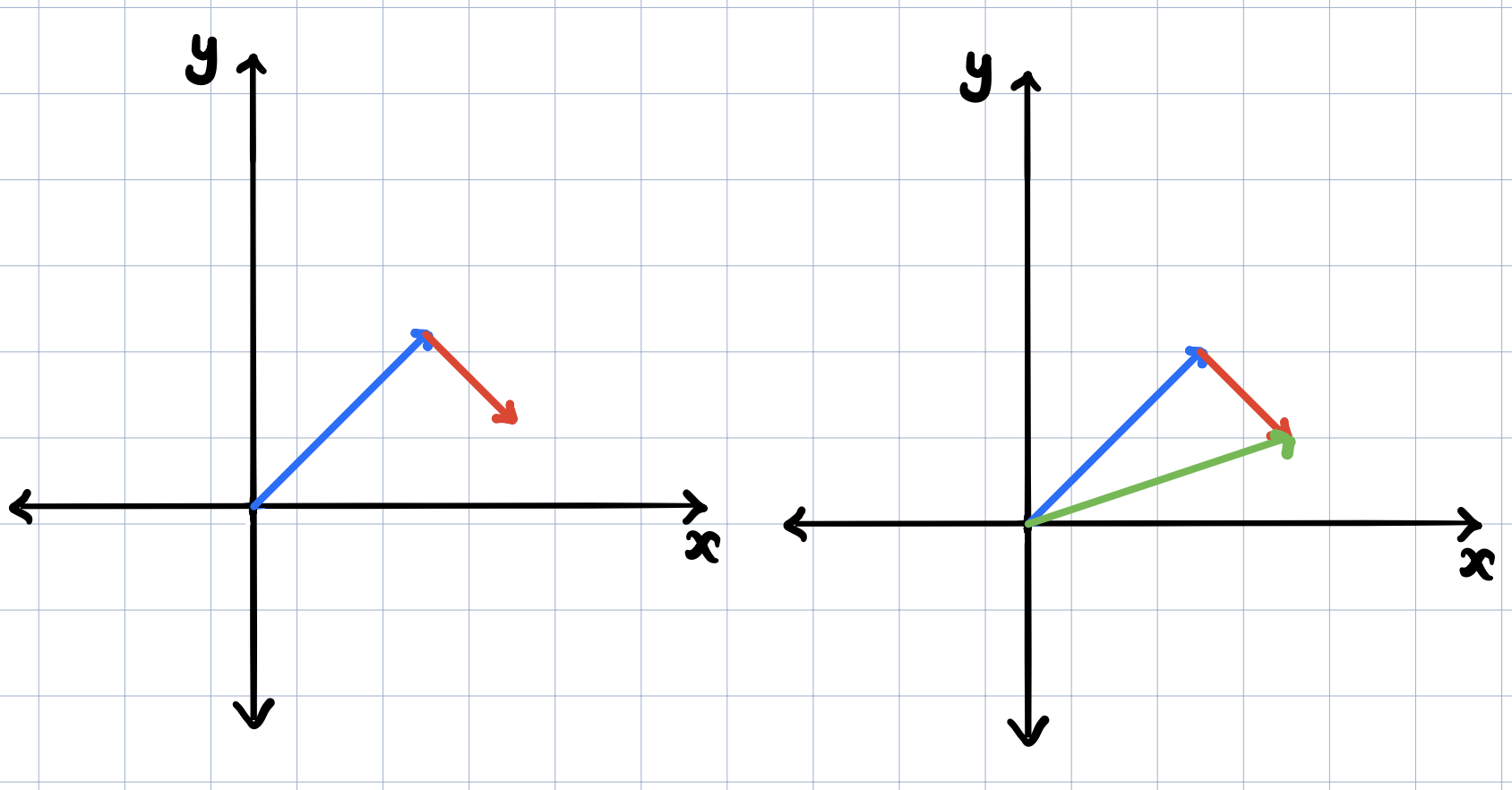
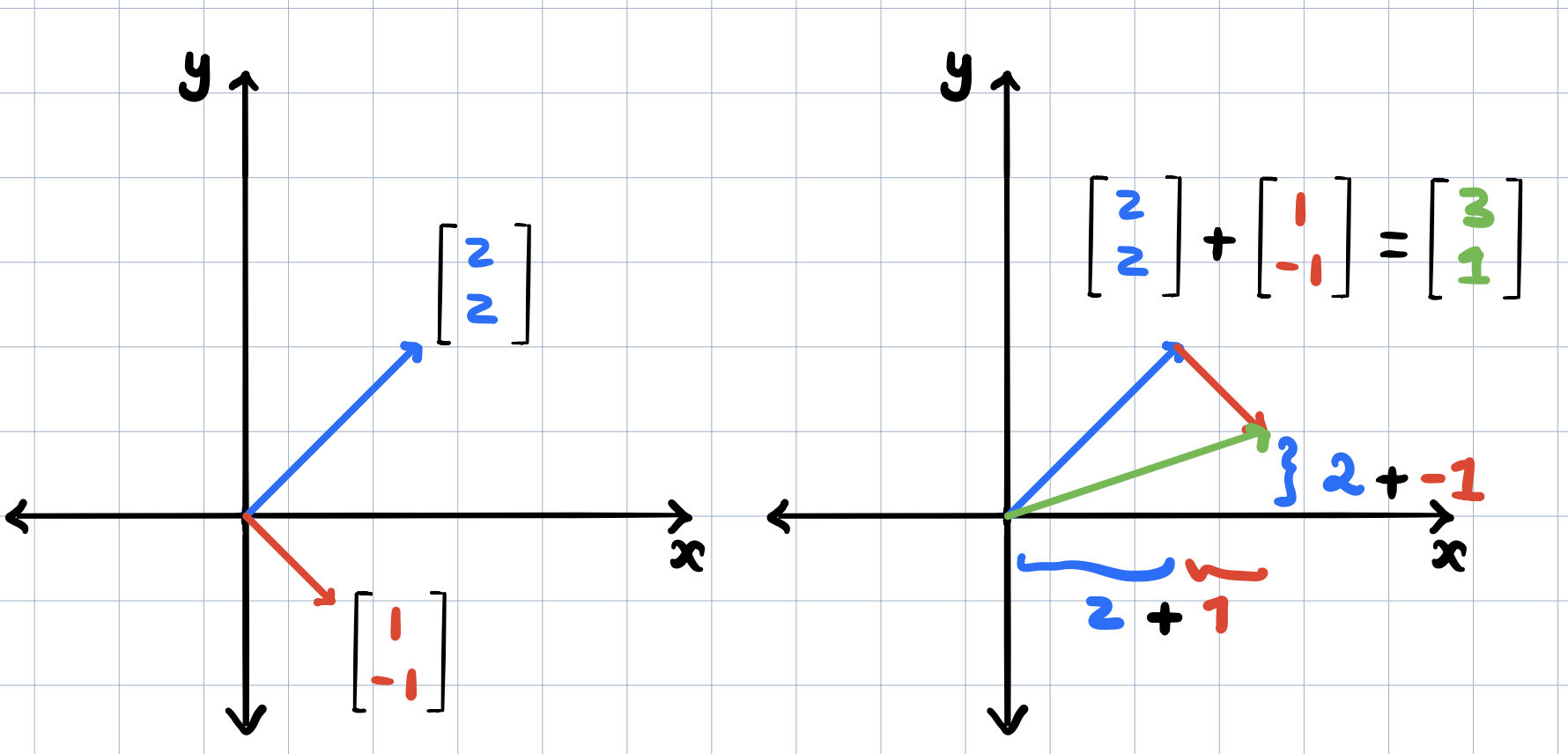
Why was addition defined this way? A vector represents a movement or a step with a direction and a distance in space. So here, if we take a step along the first vector and then take another step in the direction of the second vector and by the amount equal to the distance of the second vector, then the overall movement would be the same as moving alone the vector that represents their sum above. You can see this in the second figure below. The green vector is really the sum of the amount the first vector moved in the x-axis’s direction plus the amount that the second vector moved in the x-axis’s direction. Similarly, we add the movements in the y-axis’s direction from both vectors.
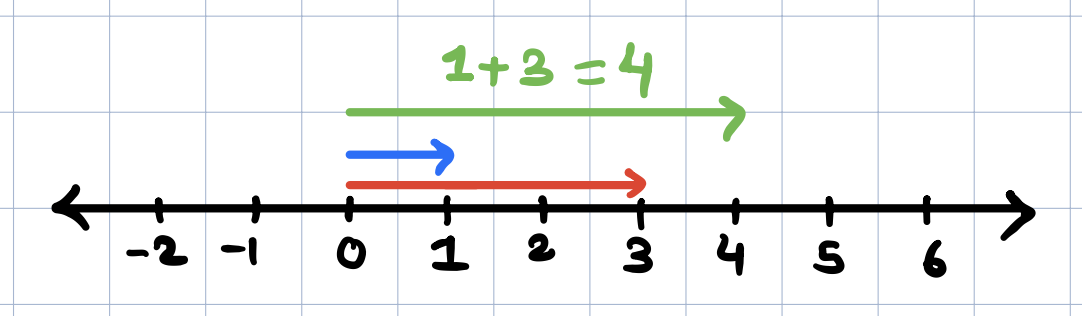
Moreover, If you think about addition of numbers on a number line, we kind of do a similar thing!
Multiplication
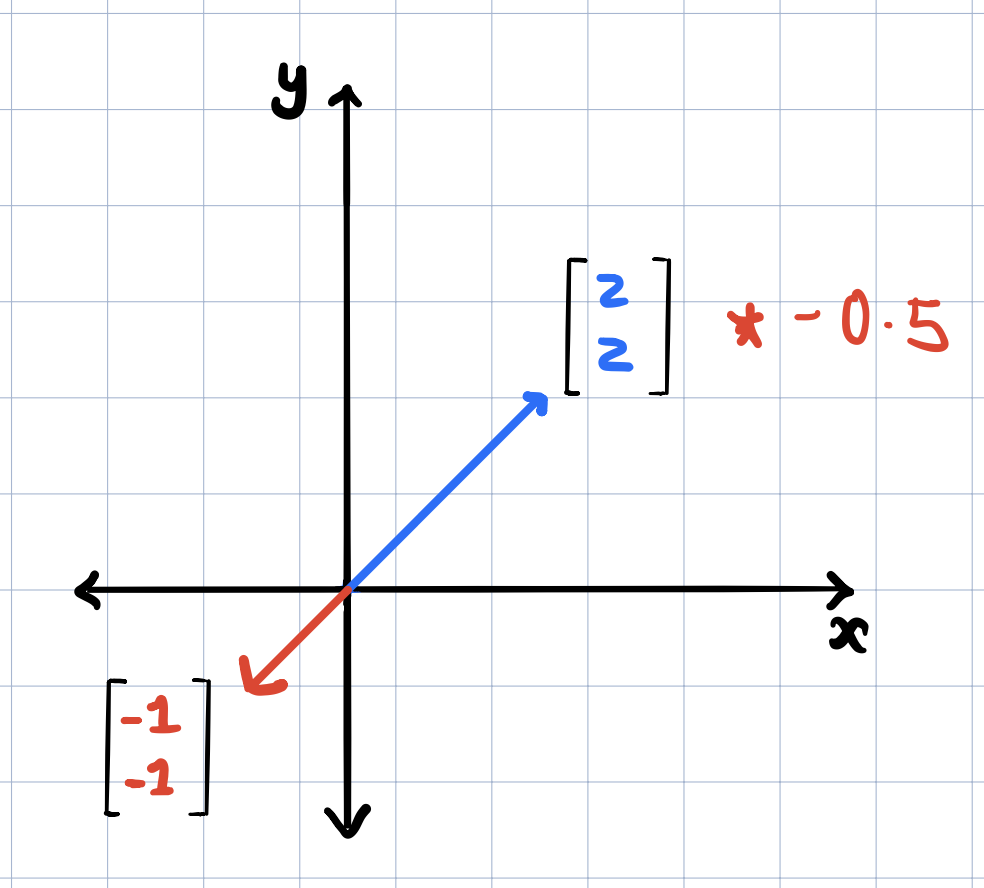
Multiplication scales a vector by the magnitude you multiply with. The magnitude is the scaler. When the sign of the vector becomes different as a result of this scaling operation, then the direction of the vector is reversed.