Convexity

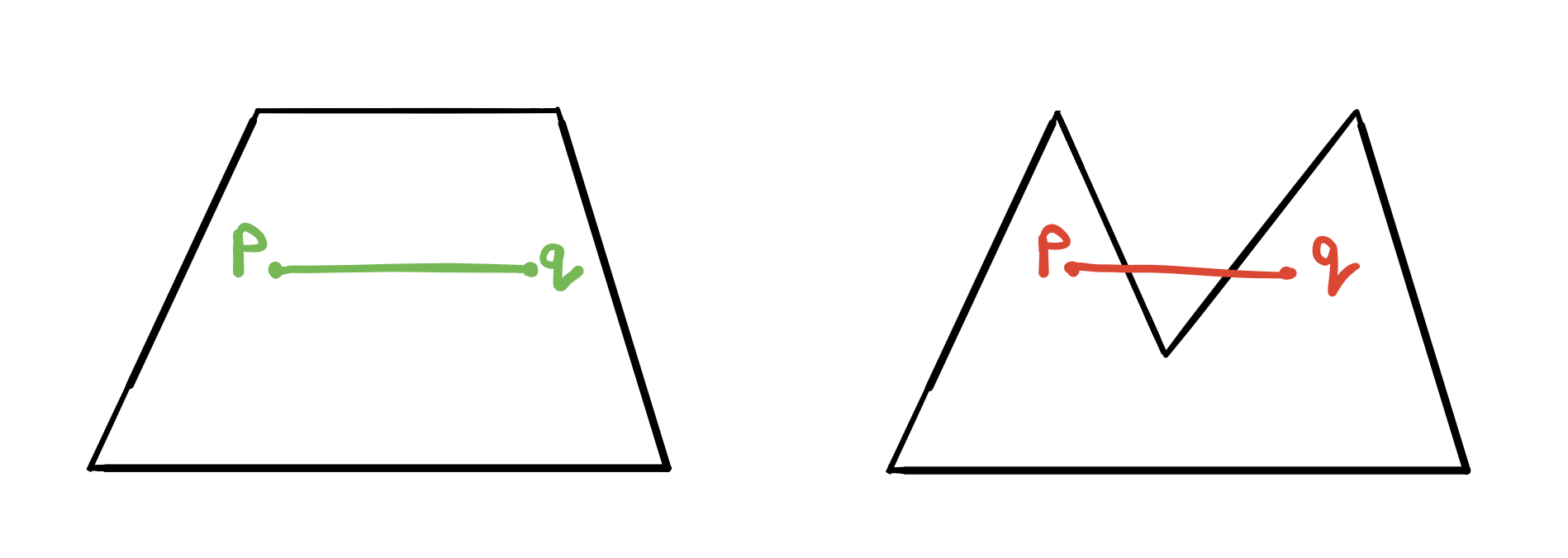
A set of points \(S\) is convex if for any two points \(p\) and \(q\) in \(S\), the line segment connecting these two points is also in \(S\) (\(\overline{pq} \subseteq S\)). A convex polygon is a polygon that is the boundary of a convex set. The left figure is a convex polygon while the right figure is not per our definition.

Convex Hull

Given a set of points \(S\), the convex hull of \(S\) is the smallest convex set that contains all the points in \(S\). This naturally implies that if we take the intersection of all convex sets of \(S\), then the result will be the convex hull of \(S\).

$$$$ \begin{align*} conv(S) = \text{ Intersection of all convex sets containing $$S$$ } \end{align*} $$$$

There are infinitely many convex sets that will contain all the points in \(S\). It turns out that this definition also works for a special kind of convex sets, called half-planes.

$$$$ \begin{align*} conv(S) = \text{ Intersection of all "half planes" containing $$S$$ } \end{align*} $$$$


Finding the Convex Hull

Finding the convex hull is a classic computatioal geometry problem and many algorithms have been developed to solve it. Next, we discuss one of the simplest algorithms that is used to find the convex hull of a set of points.

Jarvis's March (Gift Wrapping Algorithm)

Jarvis’s March is similar to Selection Sort. In each iteration of Selection Sort, we pick the smallest element in the array and then move it to the front. Once we’re done, we’ll have a sorted array. In Jarvis’s algorithm, the smallest element in each iteration is the vertex that is furthest to the right from the last vertex that was added to the convex hull. There are two main steps.

  1. Find the left most vertex
  2. Find the next vertex in the hull and repeat this until we're done.


1. Pick the Left Most Vertex

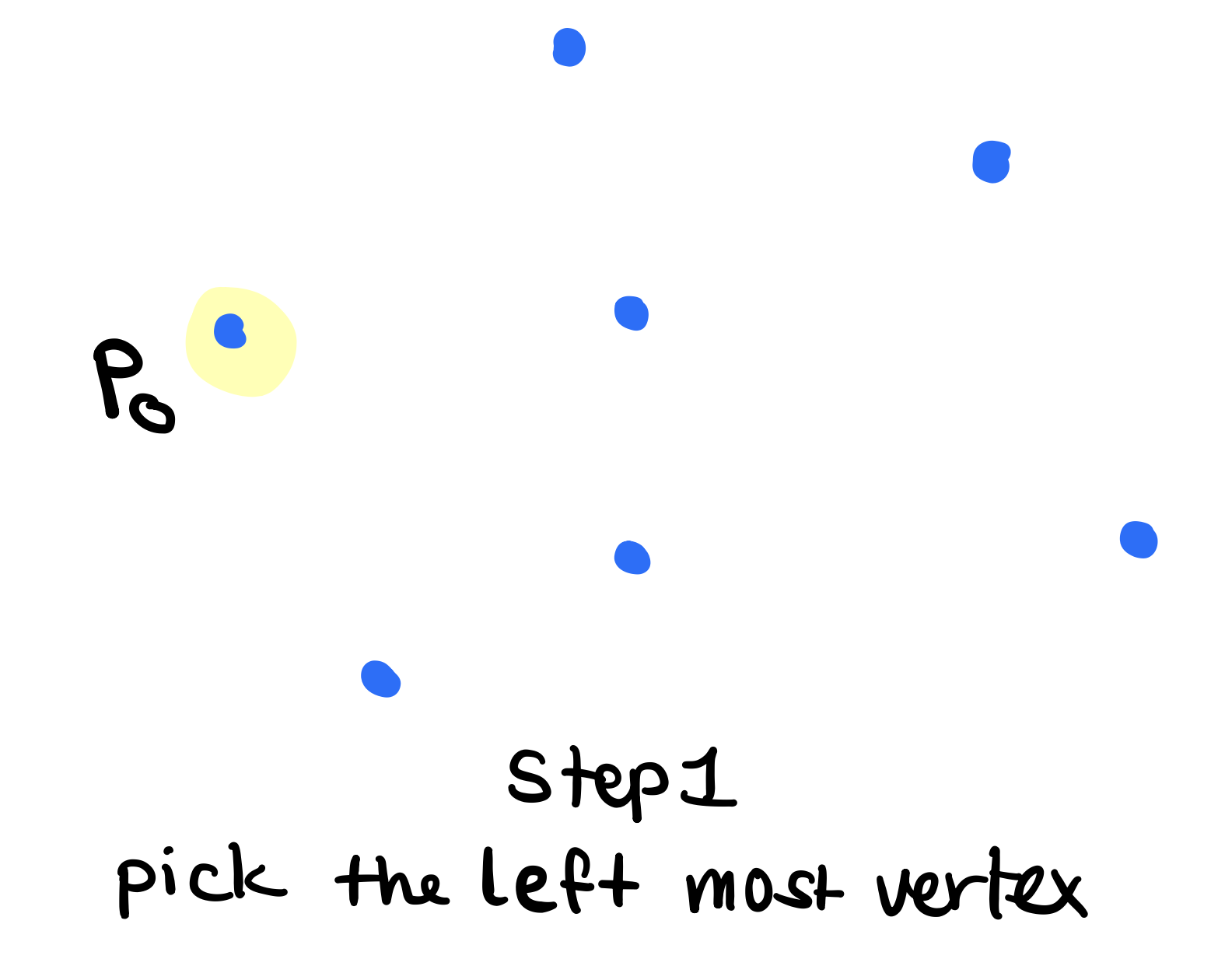
Initially, we will pick a vertex that we know will be in the hull. We can pick the left most vertex or the bottom most vertex or any vertex where all the points will be on one side (half plane). Let’s pick the left most vertex and let it be \(p_0\).



2. Pick the Next Vertex in the Convex Hull

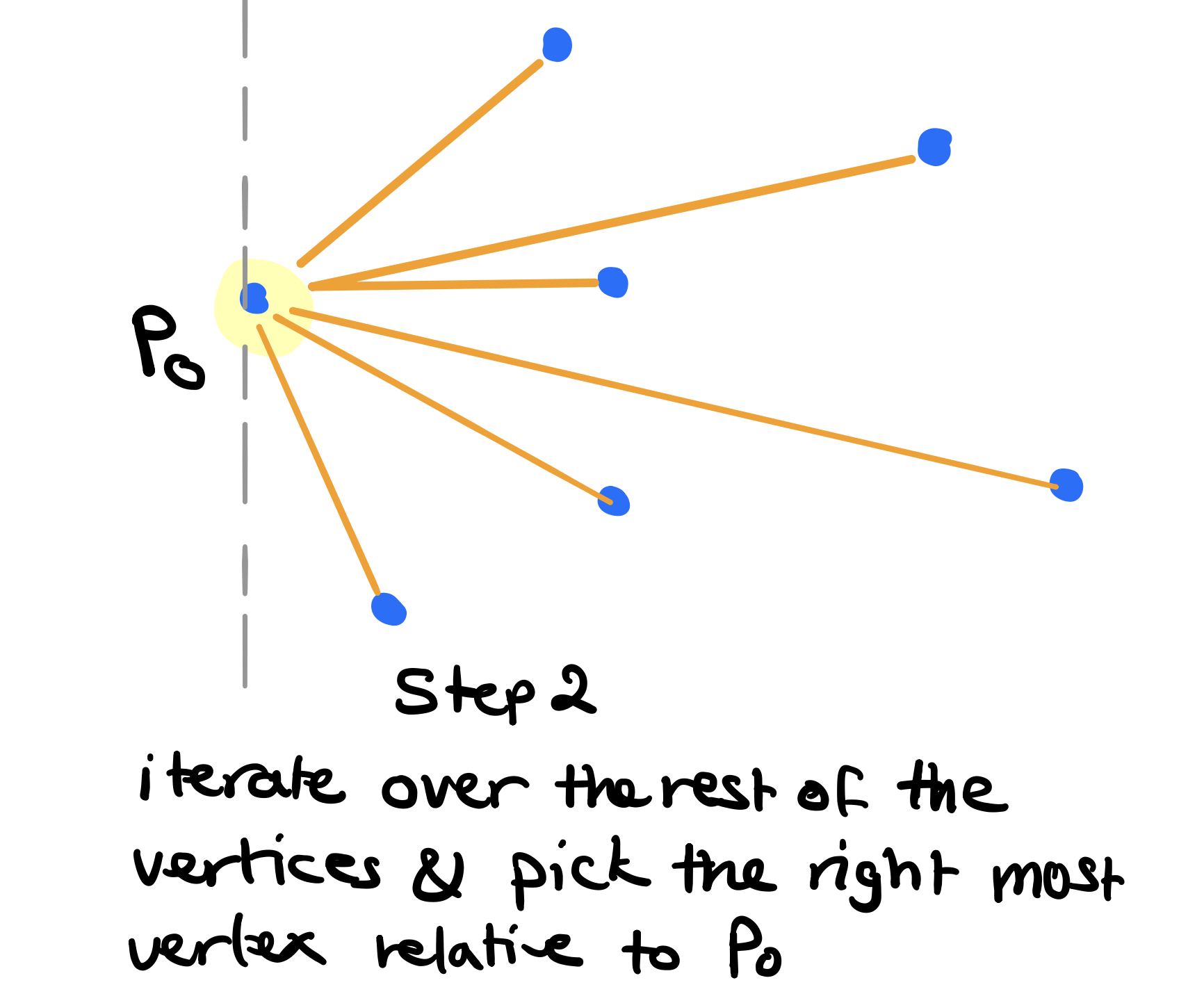
Step two is about picking the next vertex in the hull and doing so until we find all of them. To do so, imagine shooting a ray from \(p_0\) to each of the remaining vertices (figure above). The next vertex in the hull is the vertex that is furthest to the right relative to \(p_0\). How do we determine which vertex is furthest to the right?. Before exploring this, let’s define two variables:

  • \(p\) will track the last point that was added to the hull. \(p\) is initially \(p_0\).
  • \(q\) will track the current right most vertex relative to \(p\). \(q\) will be initialized to \(p + 1\) at the beginning of each iteration.

We will iterate through the vertices while updating \(q\) whenever we come across a vertex that is furthest to the right from \(p\).

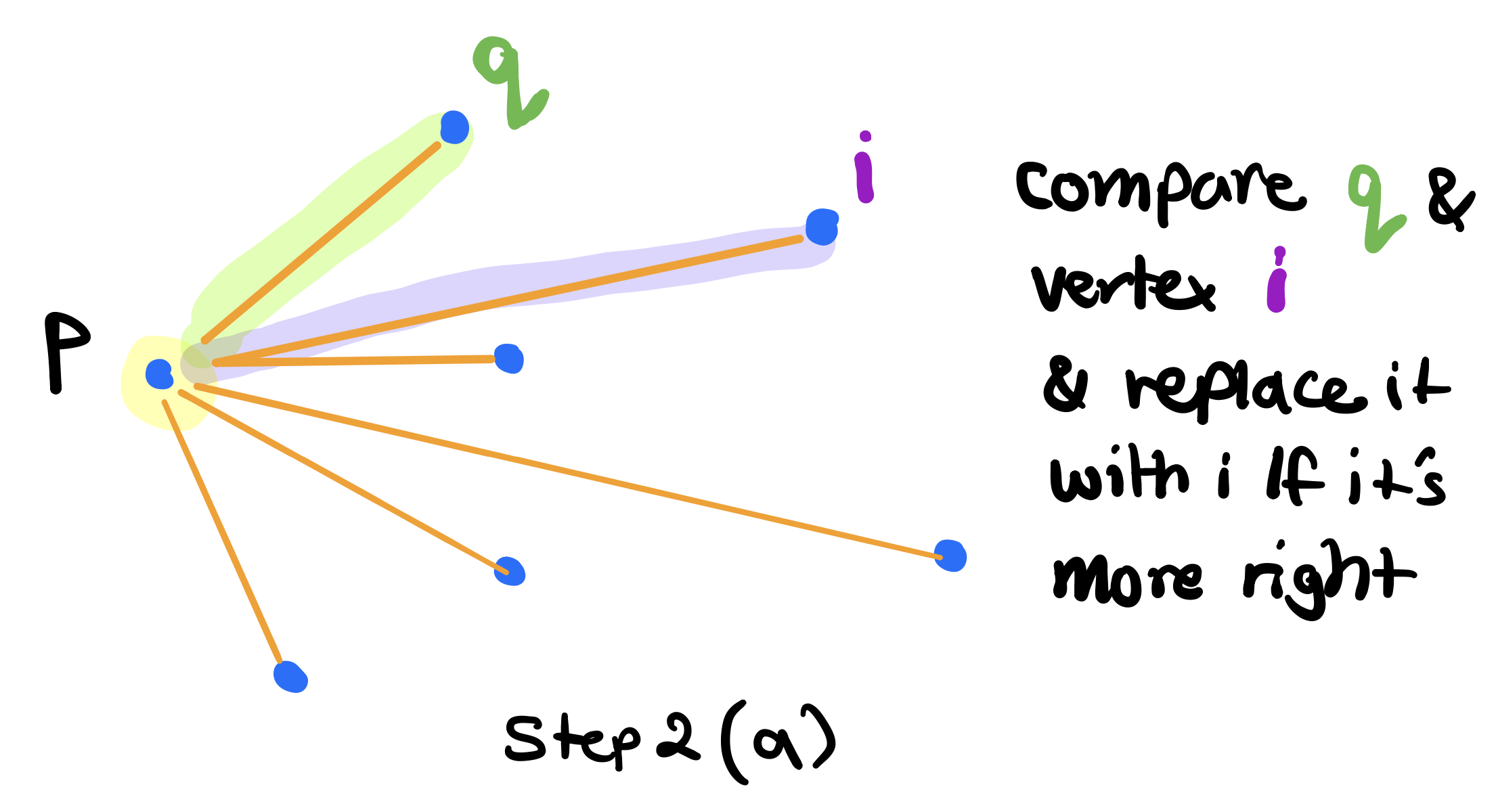
To test if vertex \(i\) is furthest to the right than \(q\), we will use the orientation test that we previously developed when triangulating a polygon. (See Orientation of Three Points). Precisely, we’ve derived an expression to find out whether a point \(r\) is on the left or right of the line that goes through two given points \(p\) and \(q\). We can wrap this expression in the function below.

// determines if r is on the left of the line pq
int direction(p, q, r) {
    int product = (q_x-p_x)(r_y-p_y) - (r_x-p_x)(q_y-p_y);
    if (product > 0) {
        return 1; // anti-clockwise
    } else if (product < 0) {
        return -1; // clockwise
    }
    return 0; // collinear
}

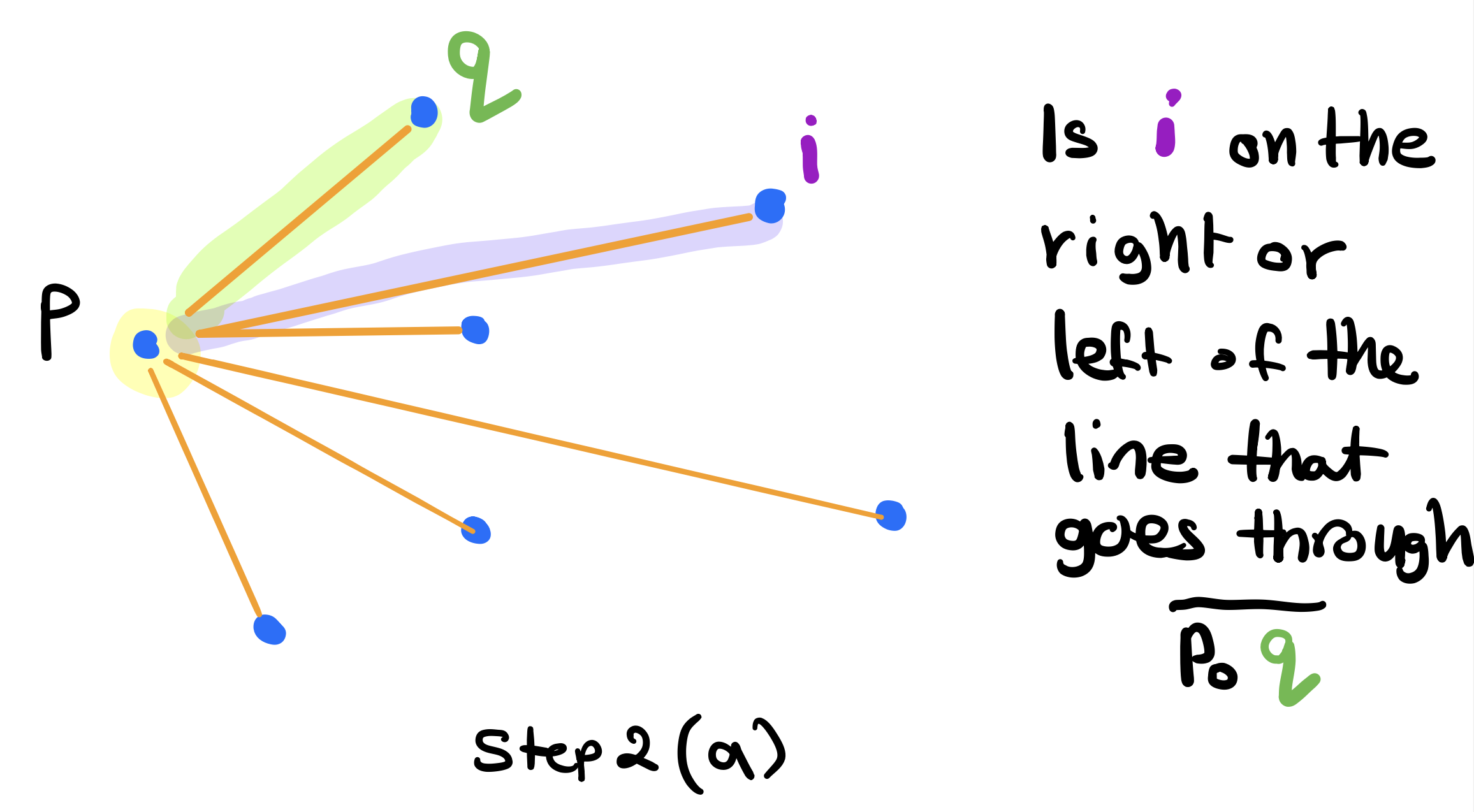
We can see above that \(i\) is indeed more to the right of the line and hence furthest to the right from \(p\). So now we set \(q\) to \(i\) and move on to test the next vertex.

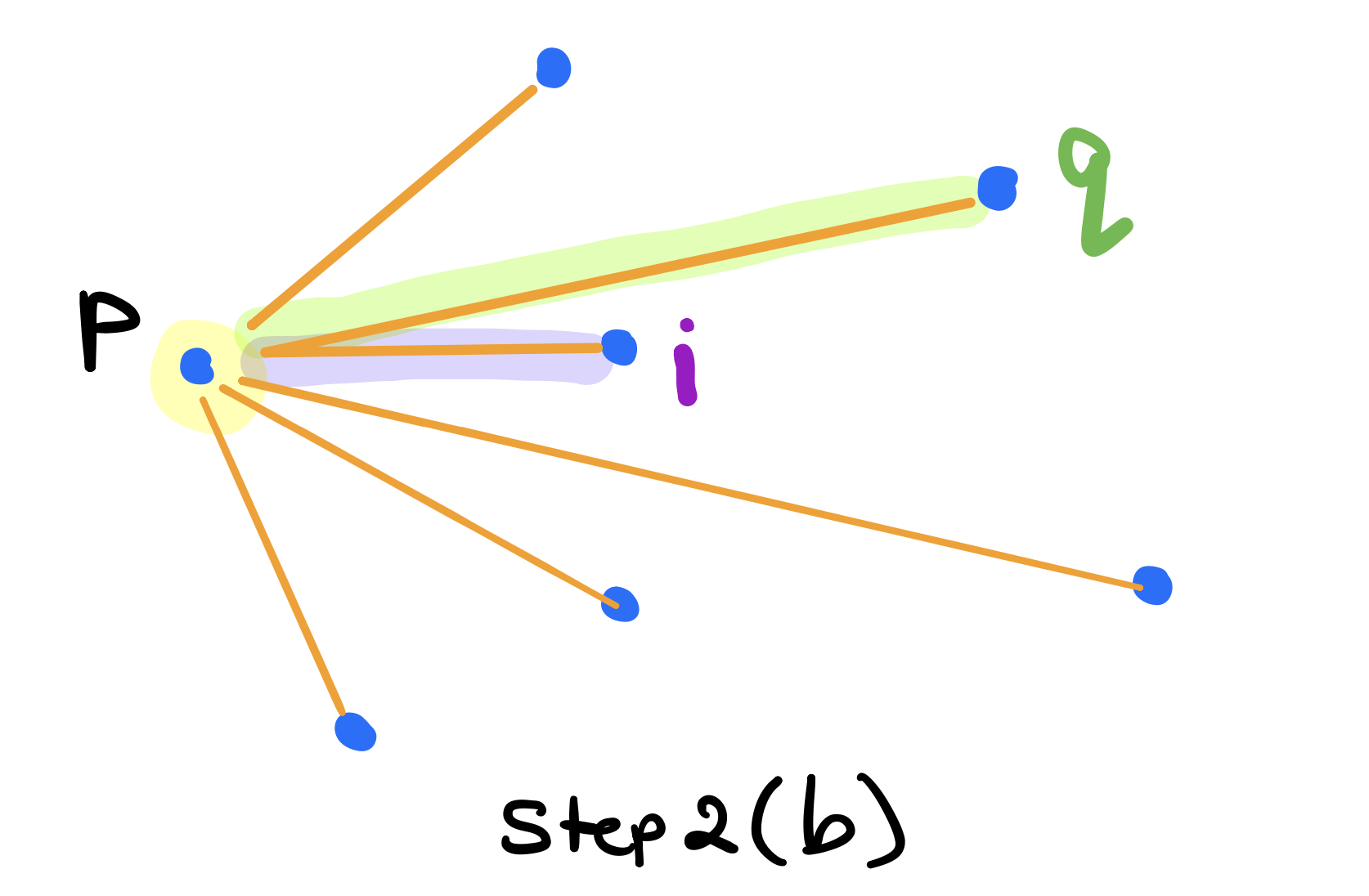
After we’re done testing all the vertices, \(q\) will be the right most vertex relative to \(p\).

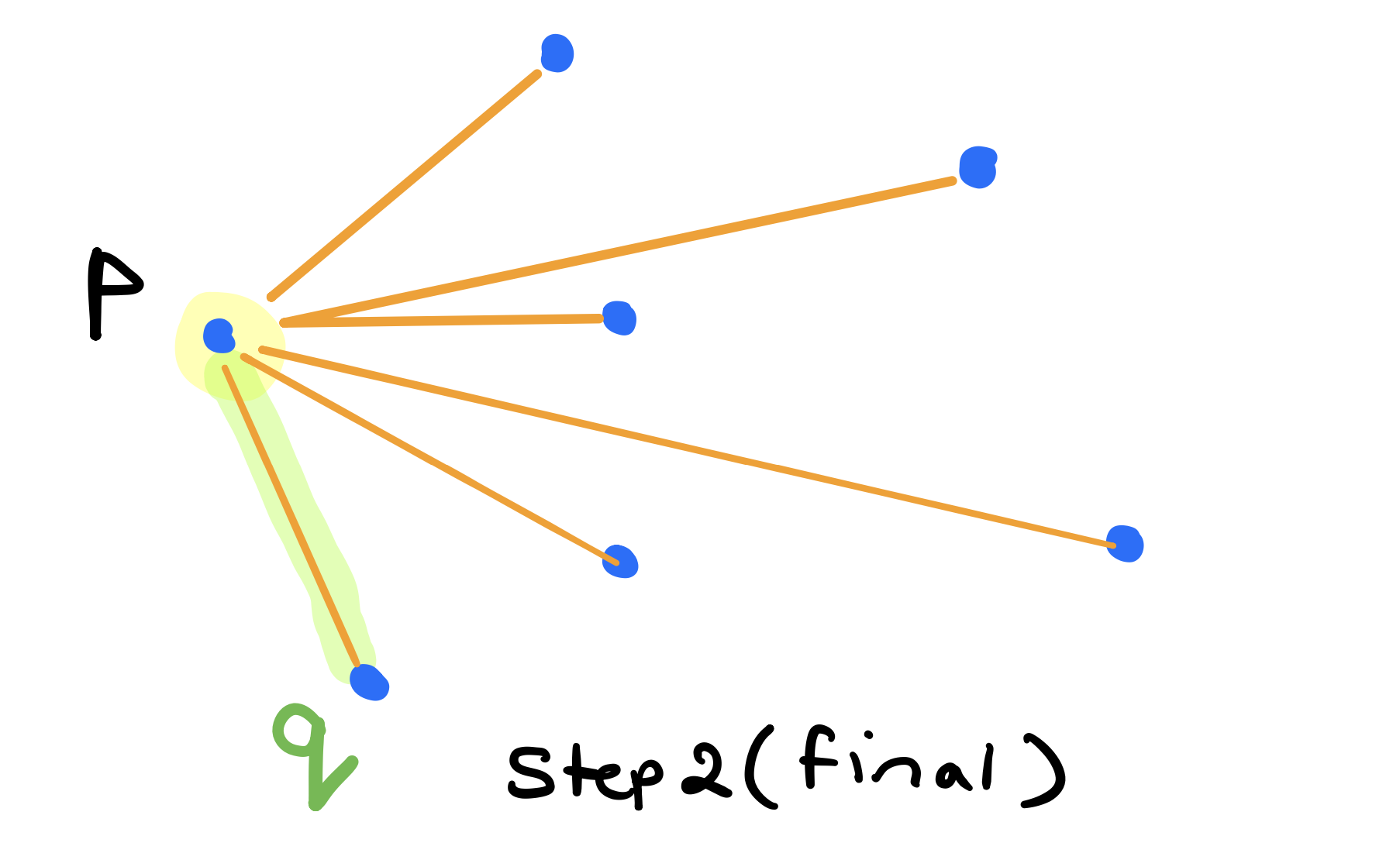
At this point we will

  • Add \(q\) above to the convex hull.
  • Set \(p\) to \(q\). (the last vertex added to the convex hull is \(q\))
  • Set \(q\) to \(p + 1\). (The next vertex in the set of vertices not on the hull yet).

The pesudo code below shows an outline of what we’re doing each step or iteration. The outer loop sets the initial \(q\) to \(p+1\) later on adds it to the convex hull when we’re done with the inner loop. The inner loop will test all the vertices and update \(q\) whenever we find a better vertex.

while (p != first_point_on_hull) {
    // (1) initialize q
    q = p + 1
    // (2) iterate through each vertex i and update q if necessary 
    for i in 1...size(S) {}
        if (orientation(p, q, i) < 0) {
	        q = i
	    }
	}
    // (3) add q to the convex hull and set p to q
    convex_hull.add(q)
    p = q
}


3. Termination

When do we terminate? We terminate when the next vertex that we want to add to the convex hull is actually the first vertex that we added to the hull. Once we get to this point, then we terminate and return the convex hull points.



Running Time

How fast is Jarvis’s March? The inner loop goes over \(O(n)\) vertices. The outerloop really depends on the size of the convex hull. If we have \(h\) points in the hull, then the running time is \(O(h)\). Therefore, the overall running time is \(O(hn)\).

References

CS 498: Computational Geometry