Given a simple polygon of $n$ vertices, we define triangulation of $p$ as the process of partitioning $p$ into triangles whose vertices are the verties of $p$. The claim is that every polygon can be triangulated and the key to proving that triangulation exists is proving the existence of a diagonal.

Every polygon must have at least one strictly convex vertex

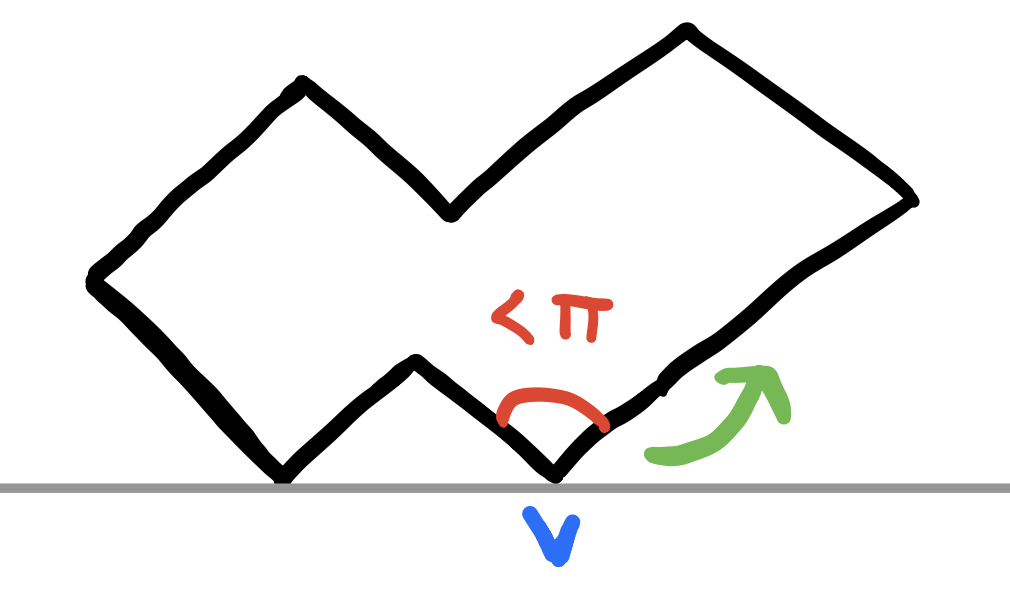
A strictly convex vertex has an internal angle that is less than $\pi$. The claim is that every polygon must have at least one strictly convex vertex.

Proof: Let $p$ be a simple polygon and let $v$ be the the vertex with the lowest y-coordinate. if there are multiple, let $v$ be the right most one. Let $L$ be the line that goes through $v$ (parallel to the x-axis?). We also know that the interior of $P$ is above $v$. If we were to traverse the boundary of $p$ then when the walker is at $v$, the previous stated conditions imply that the walker must take a left turn at $v$ and so $v$ must be a strictly convex vertex.

Lemma (Existence of a Diagonal): Every polygon of $n \geq 4$ vertices has an internal diagonal

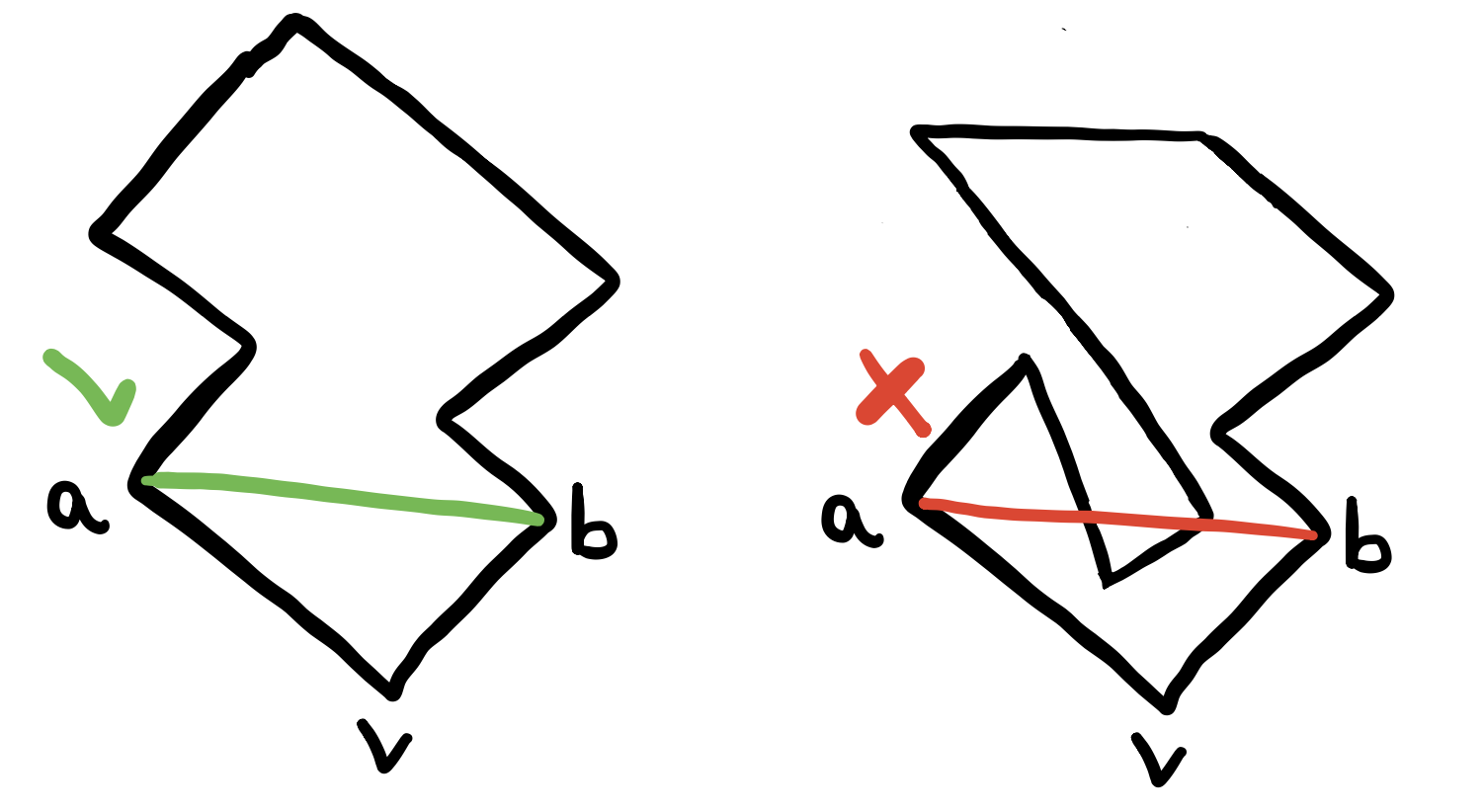
First recall from the Art Gallery post that a Diagonal is a line segment between two of the polygon’s vertices $a$ and $b$ such that the intersection of the line segment $ab$ with the boundary of the polygon ($\partial P$) is exactly the set $\{a,b\}$. We will prove that every polygon with more than 4 vertices must have an internal diagonal.

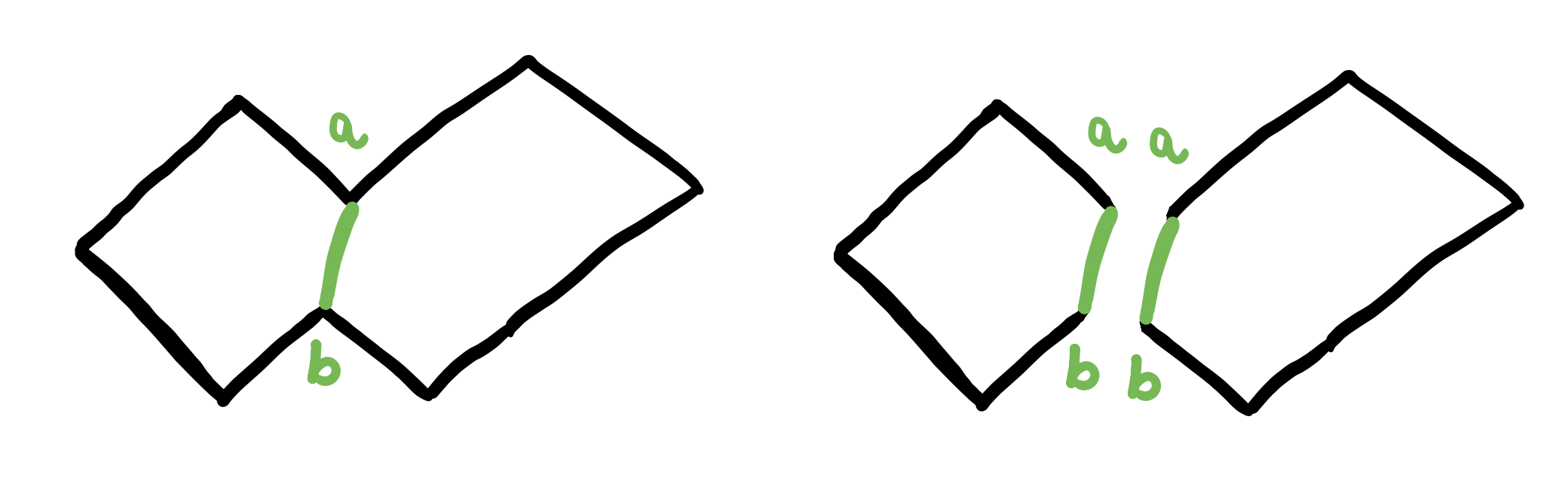
Proof: Suppose $p$ is a simple polygon. We showed previously that $p$ must have a strictly convex vertex. Let that vertex $v$. Let $a$ and $b$ be the vertices adjacent to $v$. There are two cases. If $ab$ is a diagonal, then we’re done (left figure). If $ab$ was not a diagonal, then either $ab$ is exterior to $p$ or $ab$ intersects the boundary of $p$ (right figure).

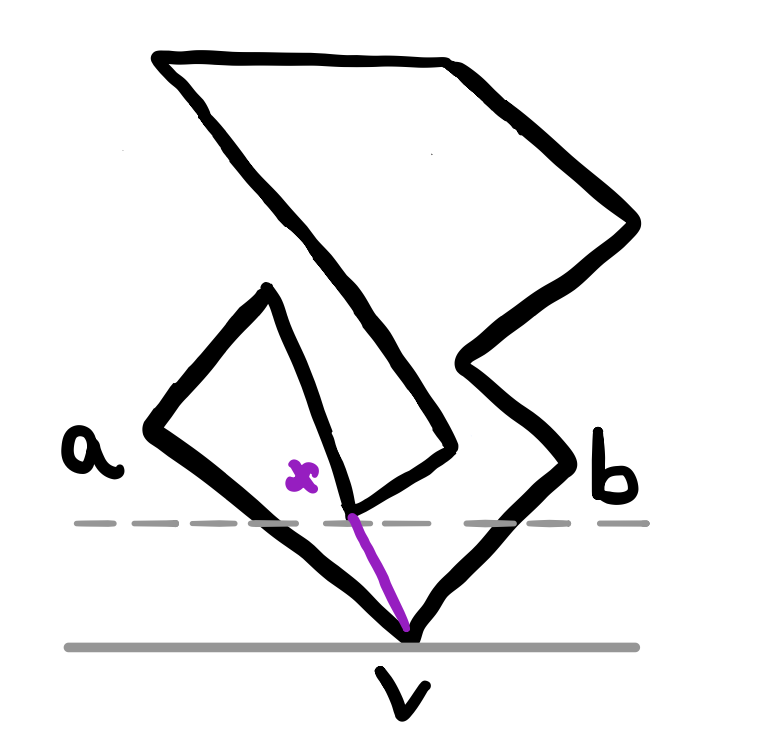
In either case, since $n > 3$, then the closed triangle $avb$ contains at least one vertex of $p$ other than $a$, $b$ or $v$. Draw a line parallel to $ab$ that goes through the vertex $v$ (It must be parallel, todo: add a picture for why it has to be). Then sweep upward from the line through $v$ until you meet the first vertex that is not $a$ or $b$. Let this vertex be $x$. Then $xv$ must be a diagonal of $p$. (TODO: MORE?)

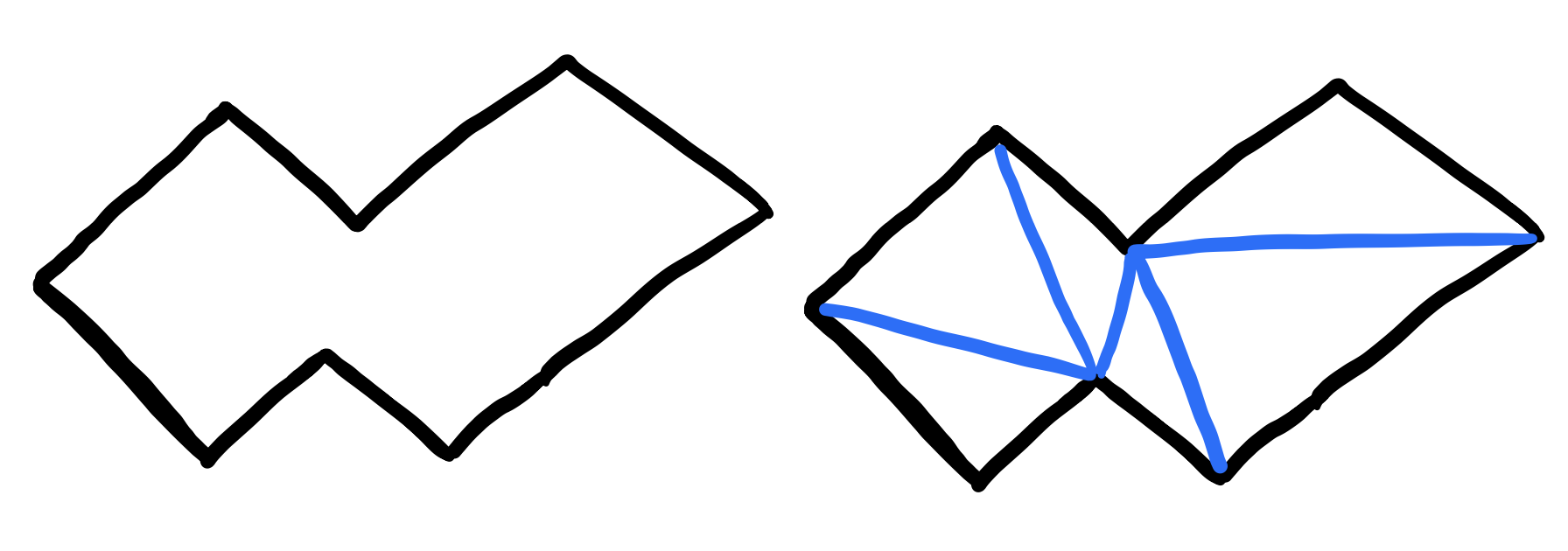
Theorem (Triangulation): Every polygon $P$ of $n$ vertices maybe partitioned into triangles by the addition of (zero or more) diagonals

Proof:

Let $p$ be a simple polygon with $n$ vertices. We will prove that $p$ can be partitioned into triangles by the addition of zero or more diagonals by induction on the number of vertices of $p$.

Base case: $n=3$, the polygon is a triangle and the theorem holds trivially ($p$ is a triangle!).

Inductive Step: Let $n>4$ and suppose the theorem is true for any polygon with fewer than $n$ vertices. By the previous lemma, we know that $p$ must have a diagonal. Let that diagonal be $d$ and let its end points be $a$ and $b$. We know $d$ only intersects the boundary of $p$ and so $a$ and $b$ are vertices of $p$. This implies that $d$ partitions $p$ into two polygons $p_1$ and $p_2$ with $d$ as edge and $a$ and $b$ vertices in both. We know that both $p_1$ and $p_2$ must have fewer vertices than $p$ since we’re not adding any new vertices in this process. It is also clear that there is at least one vertex in each part in addition to $a$ and $b$ (by the defintion of diagonal). We can now apply the induction hypothesis to $p_1$ and $p_2$ to complete the proof.

Lemma (Number of Diagonals): Every triangulation of a polygon $p$ of $n$ vertices uses $n-3$ diagonals and consists of $n-2$ triangles

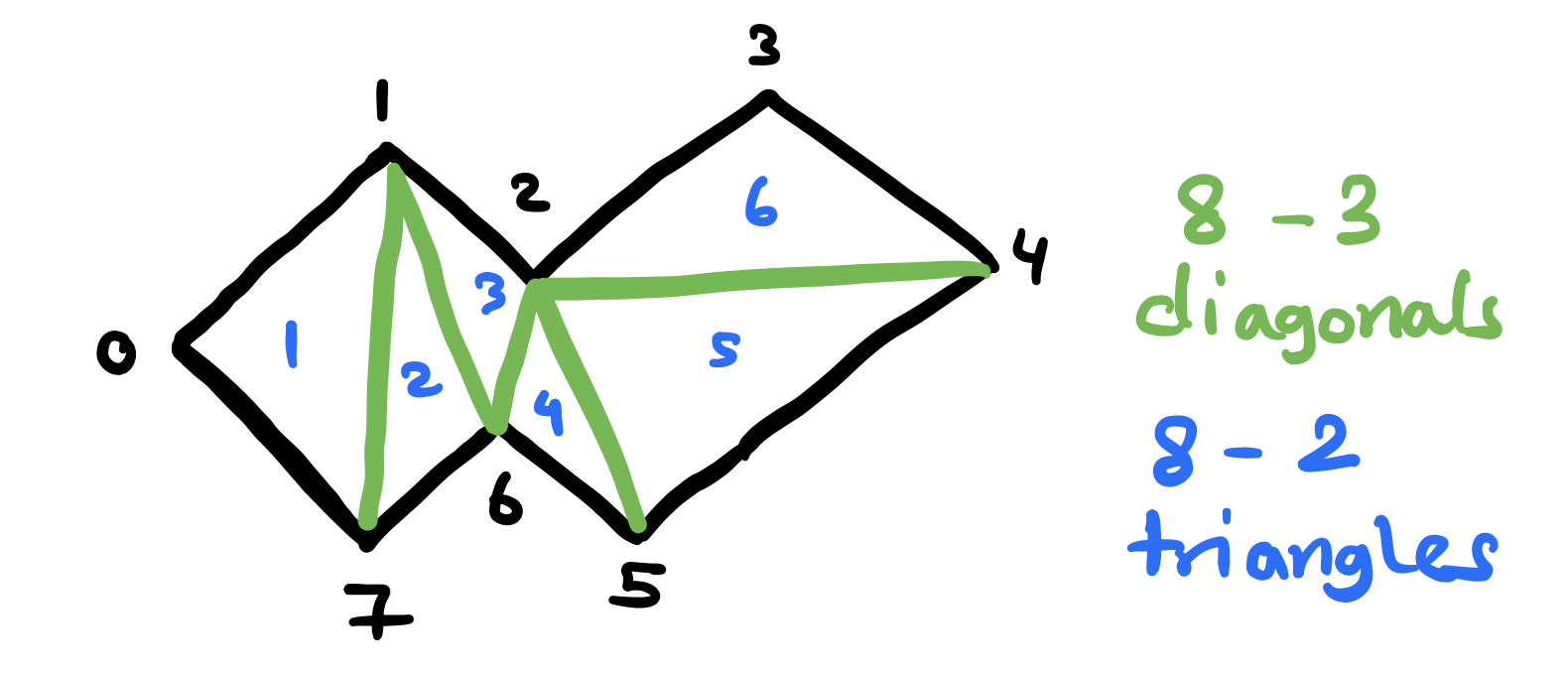
Proof: Let $p$ be a simple polygon with $n$ vertices. We will prove that the triangulation of $p$ uses $n-3$ diagonals and consists of $n-2$ triangles by induction.

Base case: $n=3$, the polygon is a triangle and the theorem holds trivially. We have $3-3=0$ diagonals and $1$ triangle.

Inductive Step: Let $n>4$ and suppose the theorem is true for any polygon with fewer than $n$ vertices. Pick a diagonal arbitrary and let that diagonal be $d$ where its end vertices are $a$ and $b$. This diagonal partitions $p$ into two polygons. Let $p_1$ and $p_2$ be the two new polygons. Let $p_1$ have $n_1$ vertices and $p_2$ have $n_2$ vertices. We know that $n_1 + n_2 = n + 2$. This is because $a$ and $b$ are counted twice in each polygon. By induction, $p_1$’s triangulation uses $n_1-3$ diagonals and consists of $n_1-2$ triangles and similarly $p_2$’s triangulation uses $n_2-3$ diagonals and consists $n_2-2$ triangles. Therefore, $p$ will have $n_1 - 3 + n_2 - 3 + 1 = n + 2 - 6 + 1 = n - 3$ diagonals and $n_1 - 2 + n_2 - 2 = n + 2 - 4 = n - 2$ triangles.

Triangulation's Dual

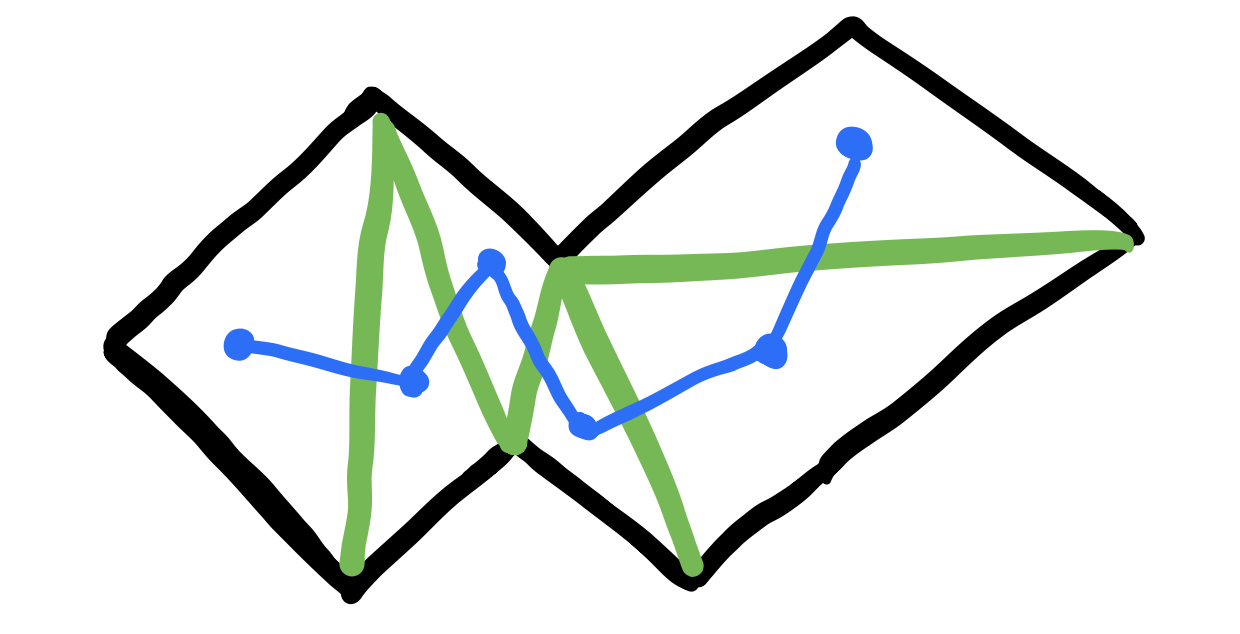
The dual of a triangulation of a polygon is a tree such that each node is associated with each triangle and an edge exists between a pair of nodes if and only if they share a diagonal. The book then states the following lemma: “The dual $T$ of a triangulation is a tree with each node of degree at most three” (TODO: Proof).

Meisters's Two Ears Theorem: Every polygon of $$n \geq 4$$ vertices has at least two non-overlapping ears

A leaf node in the triangulation dual corresponds to a an ear. A tree of two or more nodes has $n - 2$ nodes (each node corresponds to a triangle). We also know that a tree with two or more nodes must have two leaves.

References

Computational Geometry in C

Triangulation

Every polygon must have at least one strictly convex vertex

Lemma (Existence of a Diagonal): Every polygon of \(n \geq 4\) vertices has an internal diagonal

Theorem (Triangulation): Every polygon \(P\) of \(n\) vertices maybe partitioned into triangles by the addition of (zero or more) diagonals

Lemma (Number of Diagonals): Every triangulation of a polygon \(p\) of \(n\) vertices uses \(n-3\) diagonals and consists of \(n-2\) triangles

Triangulation's Dual

Meisters's Two Ears Theorem: Every polygon of $$n \geq 4$$ vertices has at least two non-overlapping ears

References