Suppose we’re given a bill of value $n=5$. We’re also given unlimited amount of coins. The possible coin values are 1, 2 and 5. What is the total number of ways of changing the bill into coins? We can exchange it for 5 coins of value 1. We can also exchange it for 3 coins of value 1 and 1 coin of value 2. Here are total possible ways: How can we design an algorithm to solve this problem?

Method 1

One way to count the number of ways to make change is to iterate through the coins and use each coin as a starting point:

  • Start with a coin of value 5, then make change for $n-5$.
  • Start with a coin of value 2, then make change for $n-2$.
  • Start with a coin of value 1, then make change for $n-1$.

When do we stop?

  • When the amount is negative, meaning this is not a valid combination.
  • When the amount is zero which means that we have arrived at a valid solution.

This is illustrated below with amount = 4 and coins 1, 2 and 5:

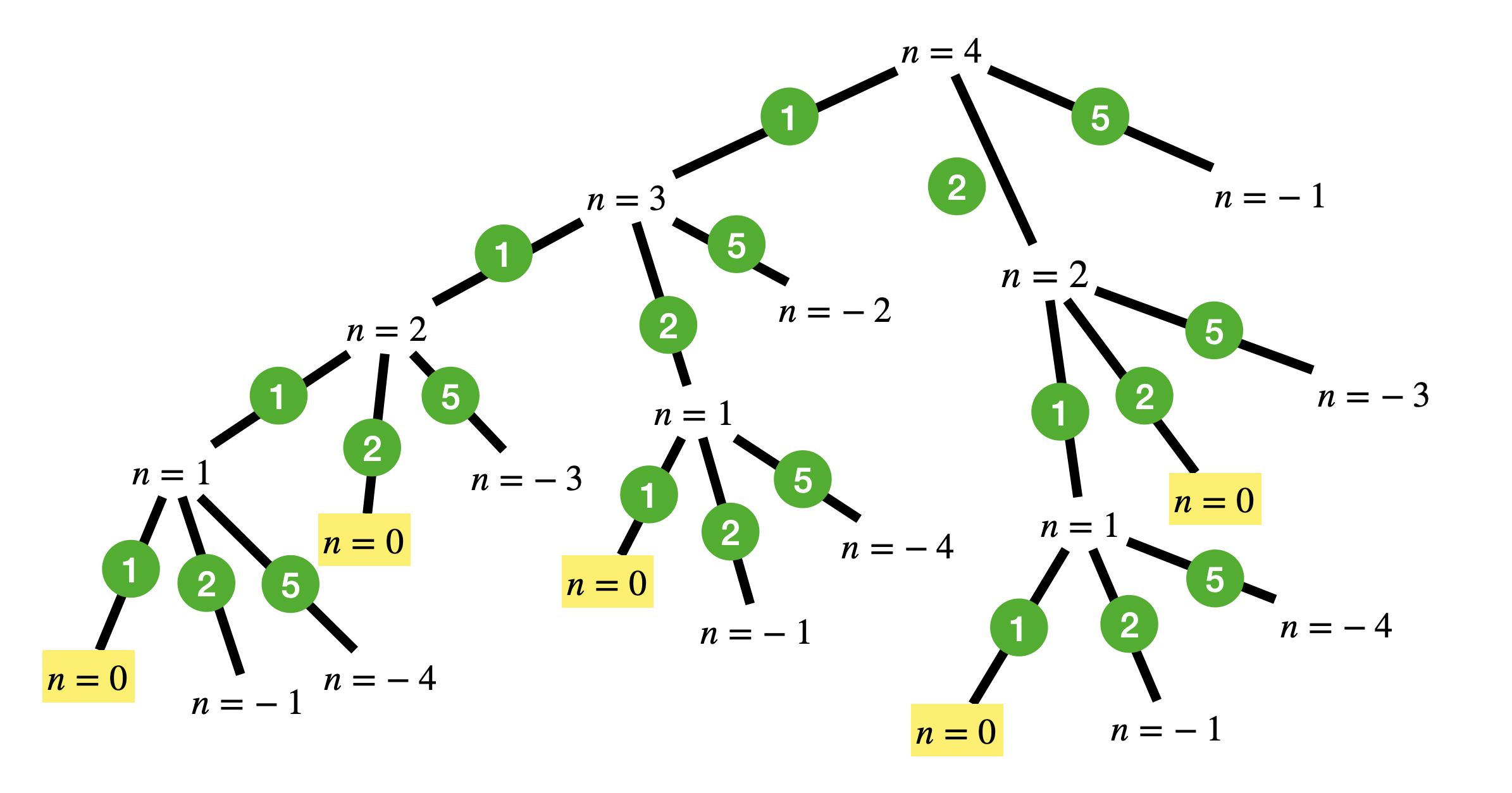
The solutions are highlighted in yellow. One thing we immediately notice is that we have duplicates! we’re finding (1,1,2), (1,2,1) and (2,1,1) as valid solutions. How can we fix this? The simplest way to fix this issue is to restrict the coins in the next iteration to coins that are less than our current coin. For example if our current coin is 2, then we only try out coins 1 and 2 at the next level. So our steps will now be:

  • Start with a coin of value 5, then make change for $n-5$ with coins (1,2,5).
  • Start with a coin of value 2, then make change for $n-2$ with coins (1,2).
  • Start with a coin of value 1, then make change for $n-1$ with coins (1).

This is illustrated below.

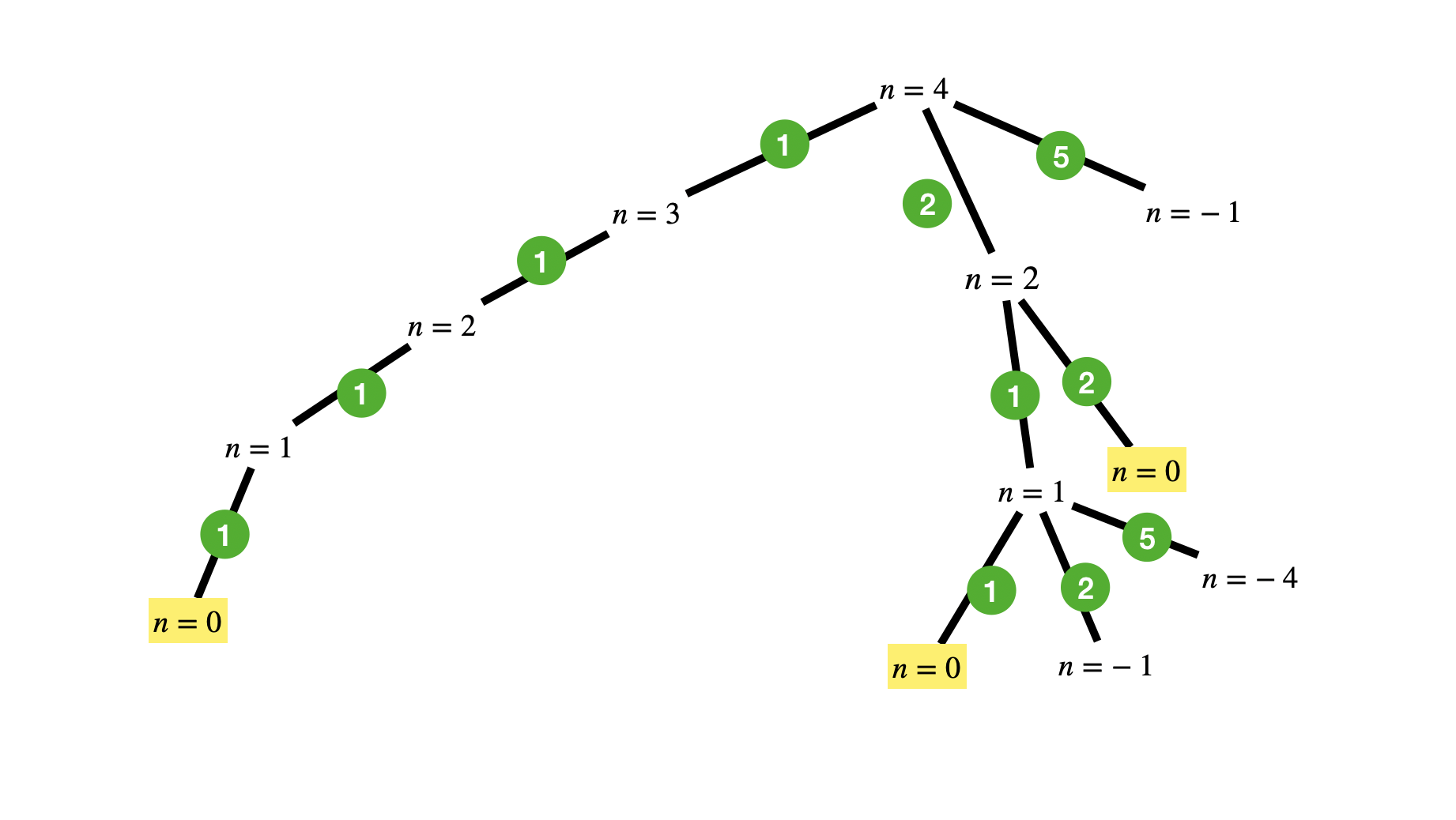
Implementation wise, we can pass an index to keep track of which coins we are allowed to use at the next level of recursion.

long make_change_recursive_alt(std::vector<int>& coins, int index, int amount) {
    if (amount == 0) { // used coins = exact amount
        return 1;
    }
    if (amount < 0) { // not the right combination of coins
        return 0;
    }
    int total = 0;
    for (int i = index; i >= 0; i--) {
        // recurse again but with the largest coin = coins[i]
        // this way we don't count duplicates
        total += make_change_recursive_alt(coins, i, amount - coins[i]);
    }
    return total;
}



Method 2

Another way to think about this problem is to divide the solutions into two sets. Fix a coin of choice, $c$, and then divide the set of solutions into solutions that use the coin $c$ and solutions that don’t use $c$. For amount 4 and coin “2”, we have 1 way that doesn’t use coin “2” and 2 different ways that does use it.

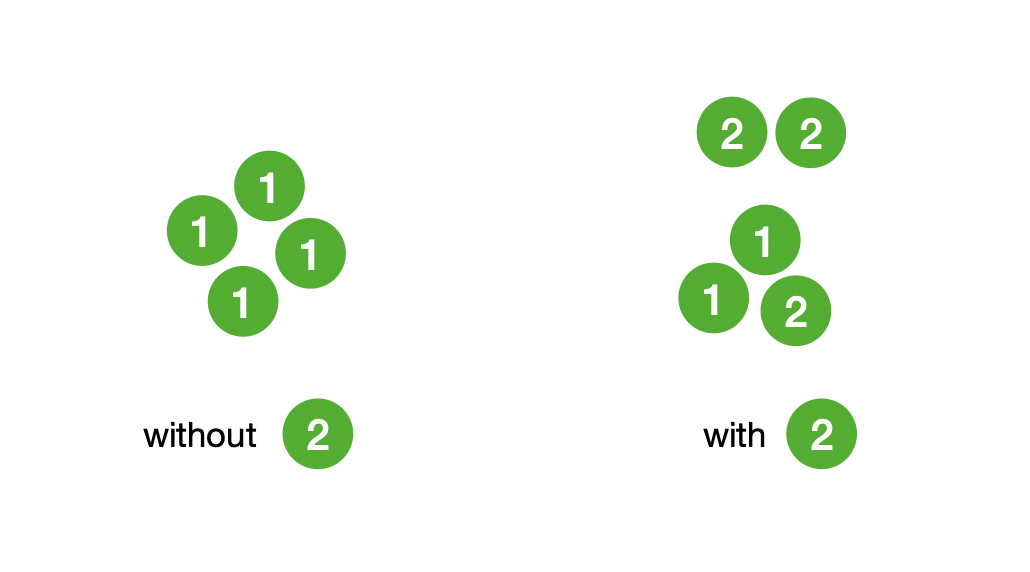
Let $K[c,n]$ be the total number of ways to make change for amount $n$ and coins $c$. Fix a coin $c_i$ from the set $c$. We will have,

$$ \begin{align*} K[c,n] = K[c-{c_i},n] + K[c, x-c_i]. \end{align*} $$

The following implementation is based on the above recurrence. Just like previously, in order not to run into duplicate solutions, we make sure to have the sequence of coins in some pre set order and then use an index to keep track of which coins we’re allowed to use in the next iteration.

long make_change_recursive(std::vector<int>& coins, int n, int amount) {
    if (amount == 0) { // used coins = exact amount
        return 1;
    }
    if (amount < 0) { // not the right combination of coins
        return 0;
    }
    if (n <= 0) { // ran out of coins
        return 0;
    }
    // either use the coin c[n-1] or don't
    return make_change_recursive(coins, n-1, amount) + // don't use this coin
    make_change_recursive(coins, n, amount - coins[n-1]); // use the coin
}

However, for $n$ coins, this solution still takes $O(2^n)$ time and is not efficient.

Method 3: Dynamic Programming

Suppose we know the solution to a problem we’re solving. An optimal substructure means that the solution will contain solutions to smaller subproblems. Does this apply to the coin change problem? Yes! we just came up with a beautiful recurrence in the recursive solution above. Let $K[c,n]$ be the total number of ways to make change for amount $n$ and coins $c$. Fix a coin $c_i$ from the set $c$. We will have,

$$ \begin{align*} K[c,n] = K[c-{c_i},n] + K[c, n-c_i]. \end{align*} $$

Both subproblems are independent of each other and both are smaller in size than the original problem.

  • The first subproblem, $K[c-{c_i},n]$, has one fewer coin.
  • The second subproblem, $K[c,n-{c_i}]$, has a smaller amount.

This is exactly what we need to implement a dynamic programming algorithm. The only thing left is to define the base case. For this particular problem:

  • $K[c,0] = 1$. The number of ways to make change for any zero amount is 1.
  • $K[0,n] = 1$ where $n > 0$. The number of ways to make change for any amount greater than zero using zero coins is 0.

It is also important just like in the recursive structure, to take care of the duplicates issue. We need to keep track of which coins we’re allowed to use.

amount/coins 0 1 2 3 4 5
0 1 0 0 0 0 0
{1} 1 1 1 1 1 1
{1,2} 1 1 2 2 3 3
{1,2,5} 1 2 2 2 3 4 
void make_change_2d(std::vector<int>& coins, std::vector<std::vector<int>>& dp) {
    // base case for amount = 0, there is 1 way to make change
    for (int i = 0; i <= coins.size(); i++) {
        dp[i][0] = 1;
    }
    // otherwise the total number of ways to make change is zero for any amount > 0 with zero coins
    for (int amount = 1; amount <= MAX_AMOUNT; amount++) {
        dp[0][amount] = 0;
    }

    for (int i = 1; i <= coins.size(); i++) { // for each coin
        for (int amount = 1; amount <= MAX_AMOUNT; amount++) { // for each amount
            // dp[n][amount] = dp[n-1][amount] + dp[n][amount-c[n]]
            dp[i][amount] = dp[i-1][amount];

            if (amount >= coins[i-1]) {
                dp[i][amount] += dp[i][amount-coins[i-1]];
            }
        }
    }
}

For amount $n$ and $m$ coins, The runtime is \(O(nm)\).

Method 4: Optimized Dynamic Programming

The previous method is great and optimal. We could however reduce the storage requirement from 2D to only 1D. If you pay attention to the recursive structure, you’ll see that each row only depends on the previous row. So what we could do is just over write the current row onto the previous row until we reach the final answer in the last row.

// bottom up with less memory
void make_change_1d(std::vector<int>& coins, std::vector<int>& dp) {
    dp[0] = 1; // base case
    for (int i = 0; i < coins.size(); i++) { // for each coin
        for (int amount = coins[i]; amount <= MAX_AMOUNT; amount++) { // for each amount, m needs to be >= c[i], start from c[i]
            dp[amount] += dp[amount - coins[i]];
        }
    }
}



Proof of Correctness

TODO?


Practice Problems

References