Combinations

Many competitive programming problems require generating combinations. For example, in 411 - Lotto, we are given \(k\) integers (all distinct) and we want to print all possible ways of choosing 6 numbers from the set. There are many approaches to generating these combinations. The following approach is a simple one.

Approach 1

In this approach, we generate all possible subsets, stopping when we reach the combination size we’re after. Suppose we’re generating $k=3$ numbers from the following set: We start generating the combinations by looking at each element starting at element “1”. We also keep track of what elements make our combination in a new array called selected. We have two choices for “1”. We either select it or we skip it. We record our selection and move down to the next level.



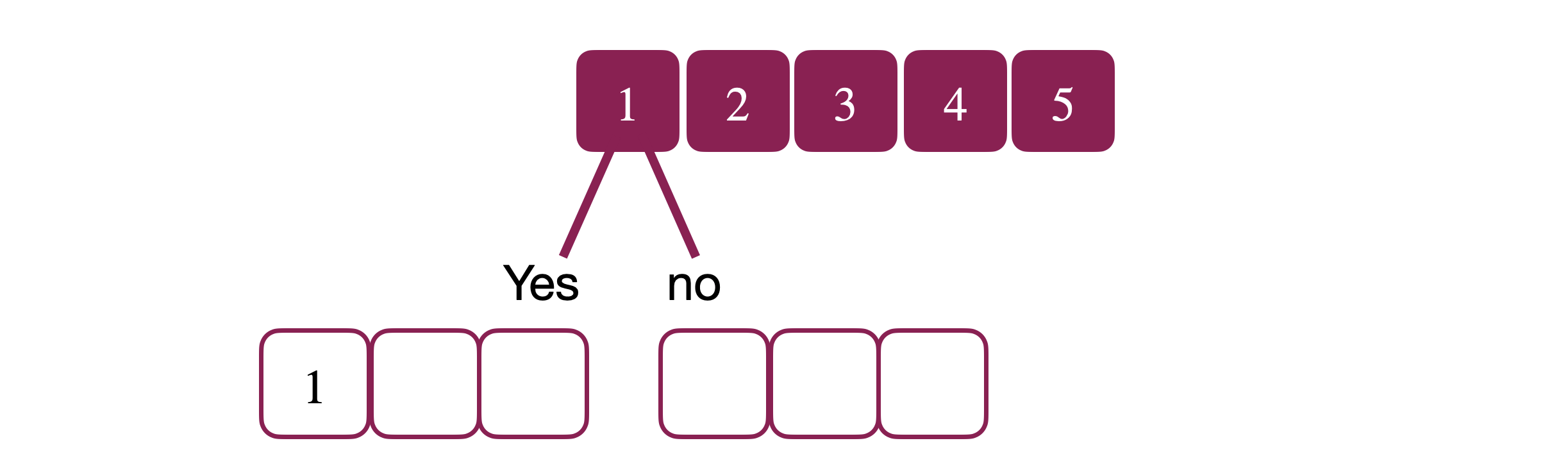
So now we’re maintaining two selected arrays, one for each choice. Next we look at “2”. We again have two choices. We either select “2” or we skip it.



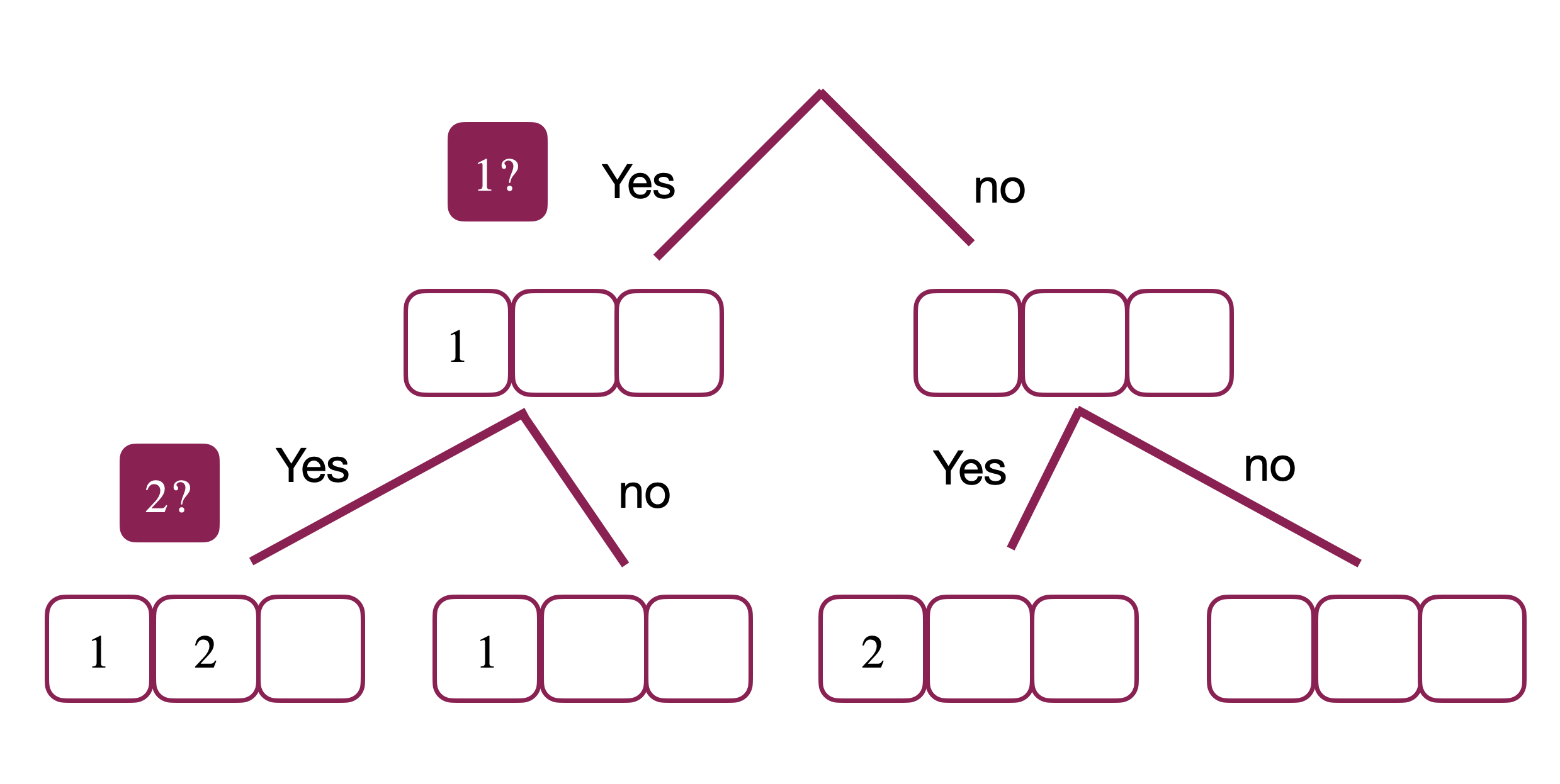
We next look at “3”. For each selected array above, we have two more choices of whether we want to add “3” or just skip it.



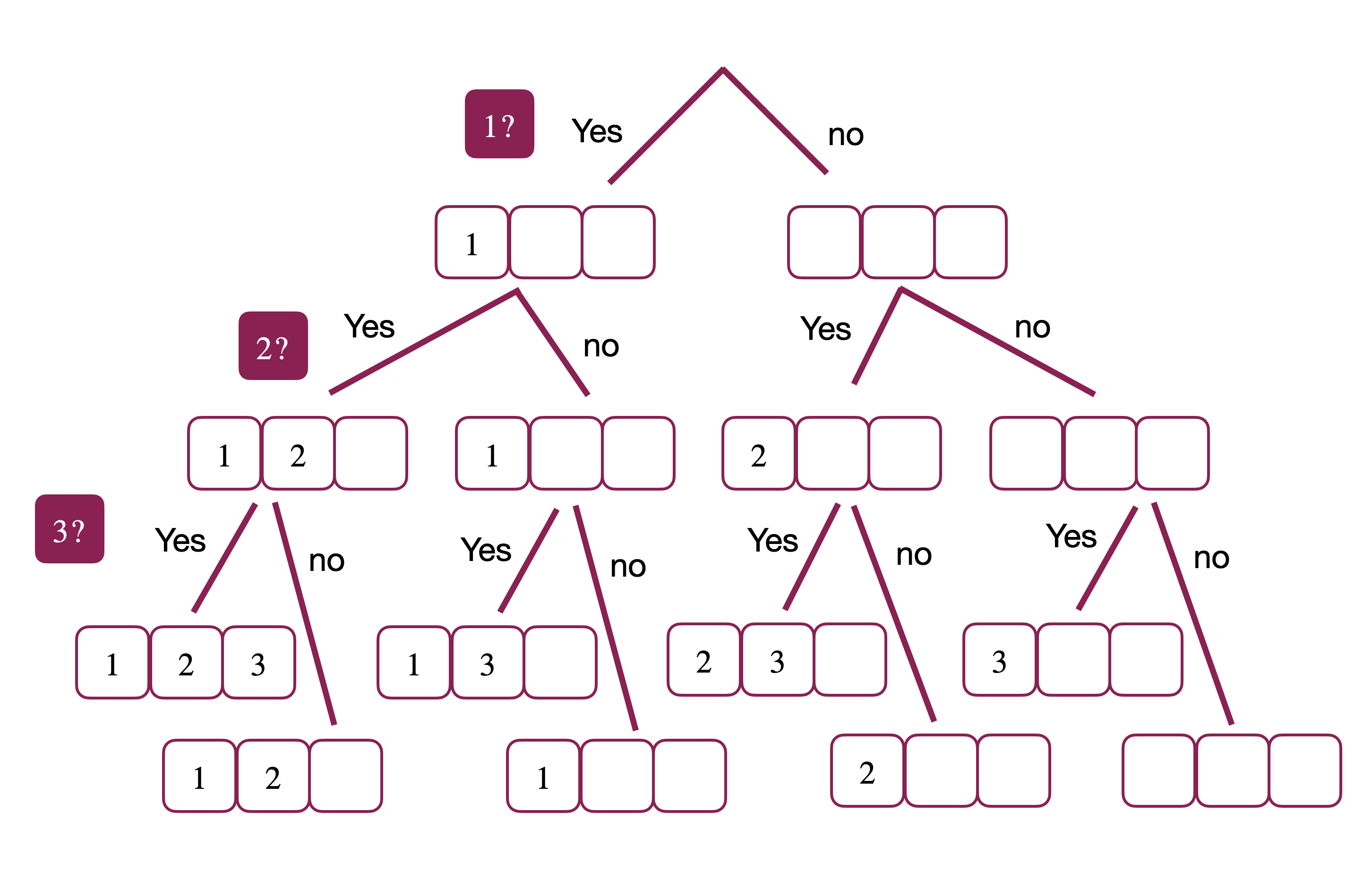
We repeat this process until one of two things happen:

• We reach \(k=3\) elements in selected and so we can print our choice and return.
• We run out of possible elements to choose and we exit.

The following code represents the process we just followed.

void combinations(std::vector<int>& a, 
                  int index, 
                  std::vector<bool>& sel, 
                  int selections,
                  int k) {
    if (selections == k) {
        print_combination(a, sel);
        return;
    }
    int n = (int)a.size();
    if (index >= n) { return; } // no more elements
    // two choices
    // (1) select a[i]
    sel[index] = true;
    combinations(a, index+1, sel, selections+1, k);

    // (2) don't select a[i]
    sel[index] = false;
    combinations(a, index+1, sel, selections, k);
}

Worst case analysis

At the top level of the recursion tree (level = 0), we make one call. At level 1 we make \(2^1\) calls. At level 2, we make $2^2$ calls. The last level (level = $n-1$) would have $2^n$ subproblems. For each call, we make $O(1)$ work of selecting or not selecting the element. So the total time would be $1+2+2^2+2^3+…+2^n = 2^{n+1} - 1 = O(2^{n})$.

Approach 2

TODO

Practice Problems

• 411 - Lotto (Solution Using Approach 1)