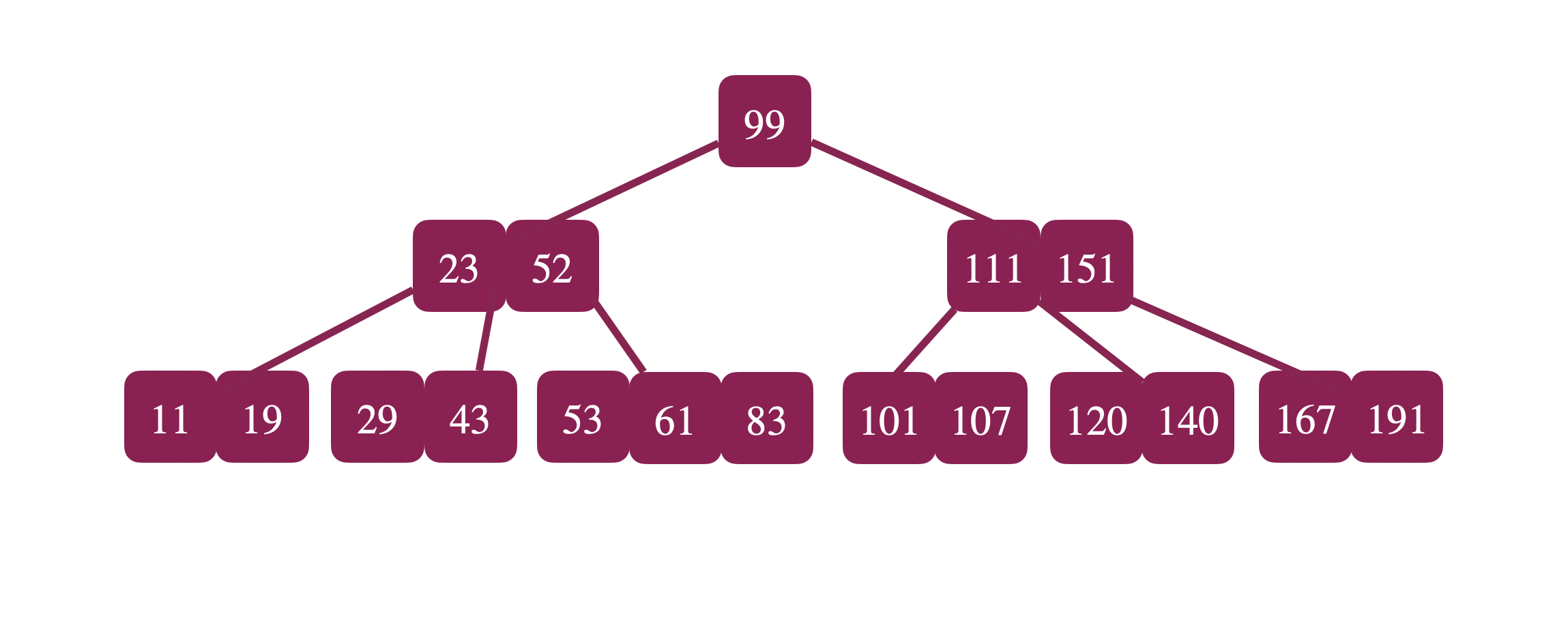
B-trees are balanced search trees. While red-black trees are also balanced search trees, their branching factor is only 2. B-trees differ in that their branching factor can be really large. The number of keys in a B-tree node determines the number of its children. A node with $n$ keys have $n+1$ children. This way, each child handles a specific range of keys in its parent.

Motivation

But why do we need a large branching factor? The motivation behind this idea has to do with minimizing disk I/O operations. Data on disk can be read in pages and so if each node’s size is a whole page in which we pack a lot of keys in, we can then minimize the number of read operations.

Specifications

Let $x$ be an internal node and let $n$ be the number of keys stored at $x$. $x$ must have $n+1$ children. Furthermore, the keys are stored in non-decreasing order. Leaf nodes on the other hand have no children. No restrictions on the number of children of the root.
The minimum degree of a b-tree is an integer, $t$ such that $t \geq 2$. Every node besides the root must have between $t-1$ and $2t-1$ keys. This also implies that it must have at least $t$ children and at most $2t$ children. If the tree is not empty, the root must be at least have 1 key.
The keys in each node are stored in non-decreasing order. The keys also define the range of keys stored in the children subtrees below. In the above figure, We see the range [0,23] defines the range for the child keys below [11,19]. Similarly [23,53] defines the range for the next child’s keys [29,43].

Why are B-trees balanced?

To see why B-trees are balanced, we will prove that the maximum height of a b-tree of degree $t$ with $n$ keys is $O(\log_t(n))$.

Proof: At level 0, the root must at least have 1 key. At level 1 we must have two children, each of which must have at least $t-1$ keys, so the total number of keys is $2(t-1)$. Each of these children will have at least $t$ children and so at level 2, we should have $2t(t-1)$ keys. Therefore, the total number of keys is at least

$$ \begin{align*} n &\geq 1 + 2(t-1) + 2t(t-1) + 2t^2(t-1) + ... + 2t^{h-1}(t-1) \\ &= 1 + 2(t-1)(1 + t + t^2 + ... t^{h-1}) \\ &= 1 + 2(t-1)\frac{t^h - 1}{t - 1} \text{ (using } \sum_{k=0}^{n}x^k = \frac{x^{n+1} - 1}{x - 1} ) \\ &= 1 + 2(t^h - 1) \\ &= 2t^h - 1 \\ \log_t(\frac{n + 1}{2}) &\geq \log_t(h) \\ h &\leq \log_t(\frac{n + 1}{2}). \blacksquare \end{align*} $$

Search

Similar to searching in a binary tree, we descend down the tree and select the right branch based on the key value. In $B$-trees, each node has has $n$ keys and so this means that we have $n+1$ children or branches. We need to compare our key with these $n$ keys to find the right child/branch to descend into.
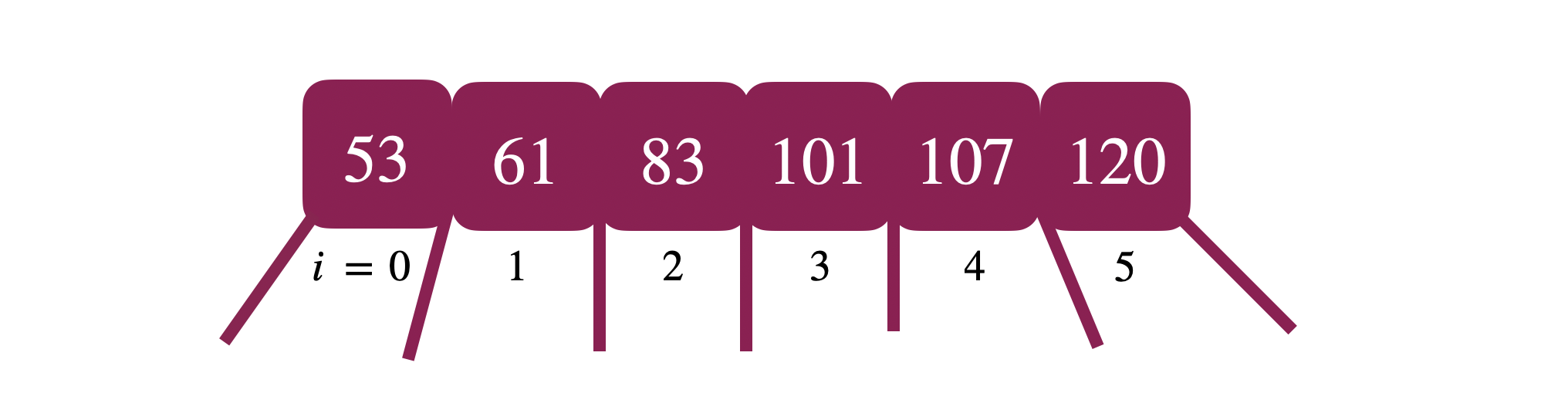
Each node stores an array of its keys. In the figure above, suppose we’re currently at node $x$ during the search and suppose we’re searching for $k = 84$. We first want to find the smallest index such that $k \leq keys[i]$. For $k=84$, the smallest index is $i = 3$. 101 is the smallest key that is larger than 84. We then have several cases:

$k = keys[i]$. This is great, we just return $x$ with the index of the key $i$.
$x$ is a leaf node so we return NULL.
$k \neq keys[i]$. $k$ falls somewhere between the key at index $i-1$ and the key at index $i$. This range corresponds to the child at index $i$. We call search again on the $i$th child.

// search a b-tree of degree t 
search(x, k) {
    int i = 0;
    // search for the smallest index such that k <= keys[i]
    // this means k will be in the range (keys[i-1], keys[i])
    while (i < x.n && k > x.keys[i]) {
        i++;
    }
    // three possible cases
    if (index < x.n && x.keys[i] == k) { // key found
        return (x, i);
    } else if (x.leaf) { // x is a leaf node
         return NULL; // no more possible matches
    } else {
        return search(x.child[i], k);
}

How long does Search take?

Note that in the above method, we were using a linear search to find the right key. For a tree of degree $t$, each node can have at most $2t-1$ keys. So this search takes $O(t)$ time. Since the tree height is $O(log_t(n))$ then the total cost is $O(t\log_t(n))$.

Suppose we instead use binary search to find the key. This means that each search will now take $O(\log(t))$ time and so the total cost becomes $O(\log(t)\log_t(n))$. Re-writing $\log_t(n)$ as $\frac{\log(n)}{\log(t)}$, we see that the total time is $O(\log(n))$.

Insert

TODO

Delete

TODO

References

CLRS
Stanford CS166