Let \(G=(V,E)\) be a directed weighted graph with \(V\) vertices and \(E\) edges. Floyd-Warshall’s algorithm is a dynamic programming algorithm that solves the all-pairs shortest paths problem in $O(V^3)$ time given that we don’t have negative-weight cycles in the $G$.
Optimal Substructure
Let \(V = \{1,2,3,...,n\}\) and consider a subset \(S = \{1,2,3,...,k\}\) such that \(S \subseteq V\) for some \(k\). Let \(i\) and \(j\) be two vertices in \(V\). Now, consider all the paths from \(i\) to \(j\) whose intermediate vertices are in \(S\). Intermediate vertices on a path are all the vertices on the path except for the start and end vertex. Let \(p\) be a shortest path among the paths from \(i\) to \(j\) that are drawn from \(S\).
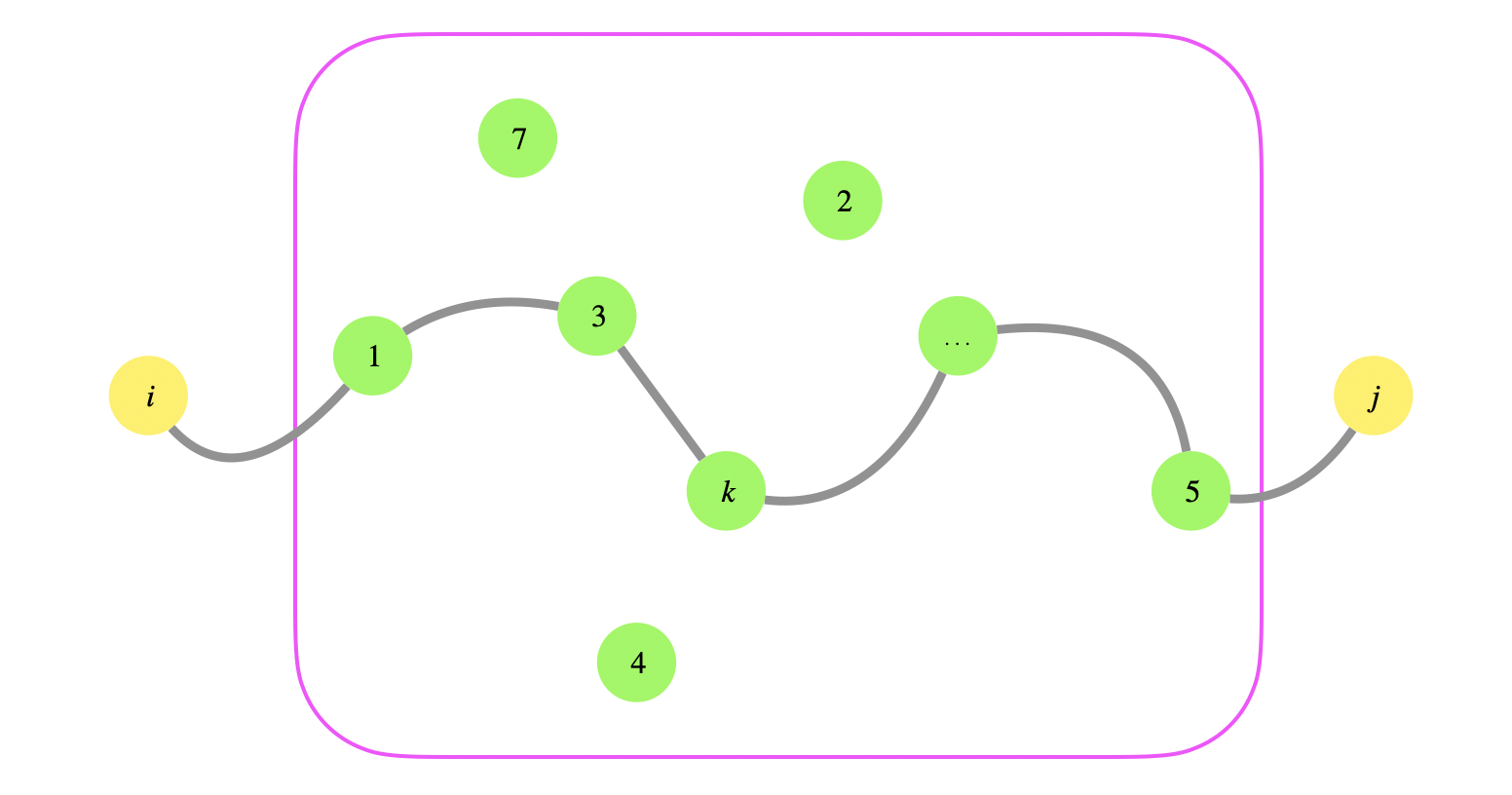 This is where it gets interesting. There are two cases here. Either \(k\) is on \(p\) or it’s not.
This is where it gets interesting. There are two cases here. Either \(k\) is on \(p\) or it’s not.
- If \(k\) is not on \(p\) then we claim that all the intermediate vertices of \(p\) are drawn from the set \(\{1,2,...,k-1\}\).
- If \(k\) is on \(p\), then we can decompose \(p\) into two shortest paths. A shortest path \(p_1\) from \(i\) to \(k\) with intermediate vertices \(\{1,2,...,k-1\}\) and a shortest path \(p_2\) from \(k\) to \(j\) with intermediate vertices \(\{1,2,...,k-1\}\). Therefore, we can derive the following:
Simple Implementation
void floyd_warshall(int n) { // O(n^3)
// the shortest path between i and j contains some internal nodes (none repeated, simple path)
// let k be an internal node, either node k is on the optimal path or it's not
// if k is on the path => the shortest distance is d[i][k] + d[k][j]
// if k is not on the optimal path => the shortest distance is dij
// if k is zero, then the shortest distance is just wij (if it exist) otherwise infinity
// (1) initialize the distance matrix
int distance[N][N];
for (int i = 1; i <= vertices; i++) {
for (int j = 1; j <= vertices; j++) {
if (i == j) {
distance[i][j] = 0; // distance from node to itself is zero
} else if (w_ij exists) {
distance[i][j] = w_ij; // current edge weight
} else {
distance[i][j] = INT_MAX; // this edge doesn't exist, set it to infinity
}
}
}
// (2) apply floyd-warshall
for (int k = 1; k <= n; k++) { // k is the internal node on the path
// for each internal node k, see if it improves the distance[i][j]
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (distance[i][k] == INT_MAX || distance[k][j] == INT_MAX) { continue; }
// current distance vs distance though k (from i to k then k to j)
distance[i][j] = std::min(distance[i][j], distance[i][k] + distance[k][j]);
}
}
}
}Also,
Full Code
Practice Problems
References
CLRS