(1) k distinguishable strings and n distinguishable buckets
Label the strings $s_1, s_2,…,s_k$ and label the buckets $b_1, b_2,…,b_n$. $s_1$ has $n$ choices of buckets to choose from. $s_2$ has $n$ choices of buckets to choose from and so. Therefore, the total number of choices is
(2) k distinguishable strings and n distinguishable buckets with at most 1 string in each bucket
Assuming $k \leq n$ (otherwise it is impossible). Label the strings $s_1, s_2,…,s_k$ and label the buckets $b_1, b_2,…,b_n$. $s_1$ has $n$ choices of buckets to choose from. $s_2$ has $n-1$ choices of buckets to choose from because it can’t go to the bucket that $s_1$ chose. Similarly, $s_3$ has $n-2$ and so on. Therefore, the total number of choices is
(3) k indistinguishable strings and n distinguishable buckets
Label the buckets $b_1, b_2,…,b_n$ and line them up below:
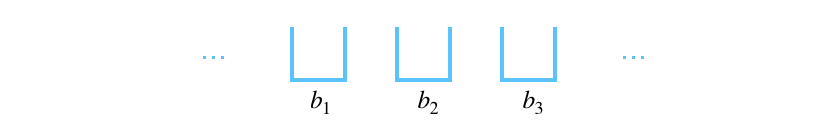 The strings are indistinguishable. We want to distribute them among the buckets so for example we could have the following:
The strings are indistinguishable. We want to distribute them among the buckets so for example we could have the following:
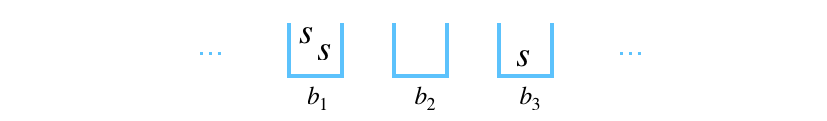 To simplify the problem, let’s pretend that they are distinguishable and instead of buckets we’ll use dividers to separate the strings into different buckets. This way the first set of strings are in bucket 1, the second set after the first divider are in bucket 2 and so on. We’ll use colors to distinguish them. We will only need $n-1$ dividers to create $n$ groups.
To simplify the problem, let’s pretend that they are distinguishable and instead of buckets we’ll use dividers to separate the strings into different buckets. This way the first set of strings are in bucket 1, the second set after the first divider are in bucket 2 and so on. We’ll use colors to distinguish them. We will only need $n-1$ dividers to create $n$ groups.
To visualize this, suppose $n=4$ and $k=5$. In the below figure, we have ${s_1,s_2}$ in the first bucket. ${s_3}$ in the second bucket. ${s_4,s_5}$ in the third bucket. The forth bucket is empty.
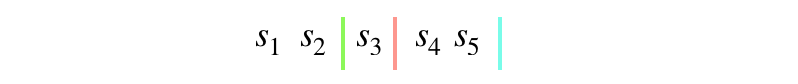 How many possible permutions are there? We have $n-1$ dividers and $k$ strings so
How many possible permutions are there? We have $n-1$ dividers and $k$ strings so
Now, since strings are really indistinguishable, let’s remove the labels. We also don’t need the colors because we’re assuming the first set of strings goes to the first bucket, the second set goes to the second bucket and so on. So we’ll have something like this:
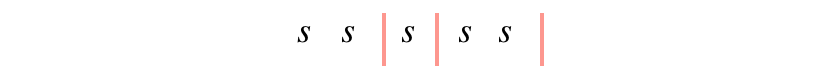 To remove the unnecessary ordering, we divide by $k!$ and also divide by $(n-1)!$. Therefore, the final answer is
To remove the unnecessary ordering, we divide by $k!$ and also divide by $(n-1)!$. Therefore, the final answer is
Note that solution can be applied to other interesting examples like finding the number of integer solutions to $x_1+x_2+…+x_k=n$.
(4) k indistinguishable strings and n distinguishable buckets with at most 1 string in each bucket
In case (2), we saw that the number of ways to put $k$ distinguishable strings into $n$ distinguishable buckets with at most 1 string in each bucket is $\binom{n}{k} * k!$. In this case, the strings are indistinguishable so we don’t care about the order of strings and so we divide by $k!$. The final answer therefore is simply
References
- Personal study notes from CS109 http://web.stanford.edu/class/archive/cs/cs109/cs109.1188/