Suppose we are given a list of $n$ two dimensional points $\{\{x_1,y_1\},\{x_2,y_2\},...\{x_n,y_n\}\}$ and we want to find the closest pair of points in the list. By closest we mean they are the closest in terms of their euclidean distance. One naive approach would be to simply iterate over all possible pairs and find out the closest pair. This algorithm has a running time of $O(n^2)$ since we have $O(n^2)$ possible pairs. What else can we do?

Divide and Conquer

The brilliant algorithm we’re about to study is a divide and conquer algorithm, meaning that we will repeatedly divide the problem into a number of subproblems and then we will repeatedly combine the intermediate results until we arrive at the final result. As a starting point we will sort the points by their x-coordinate and let that array be $P_x$. We will also sort the points by their y-coordinate and let that array be $P_y$. We will be using $P_y$ later in the algorithm. Given $P_x$. We can start by applying the following divide and conquer idea. Repeatedly divide $P_x$ into two halfs, left and right. Find the closest pair in the left half and the closest pair in the right half and then combine the results to output the single true closest pair.

How do we combine the results to find the single true closest pair? we need to consider that the closest pair might have a point in the left half and a point in the right half. We call this pair a split pair. So in the combine step we need to do two things, we find the split pair with the minimum distance. We then return the minimum pair of the three pairs we have, the left pair, the right pair and the split pair. The following pseudo-code implements this idea.

int closest_pair(Px, Py) { // Px sorted by x-coordinate, Py by y-coordinate
   if (Px has less than three points) { 
       // just use the naive algorithm 
    }
    // we will divide Px into two arrays left and right
    // median = Px[n/2-1]
    left_x, right_x = split_px_around_the_median(Px, median);

    // We want to sort each of left_x and right_x by the y-coordinate.
    // discussed next
    right_x, right_y = sort_left_and_right_by_y(Py, Px[n/2-1]);
	
    // we find the closest pair in each half
    left_pair = closest_pair(left_x, left_y);
    right_pair = closest_pair(right_x, right_y);
	
    // delta_left and delta_right are the minimum distances in the left and right halfs
    delta_left = distance(left_pair);
    delta_right = distance(right_pair);
	
    // we'll discuss this soon!
    delta = min(delta_left, delta_right);
    split_pair = find_split_pair(Px, Py, delta);

    return min(left_pair, right_pair, split_pair);
}

Running Time

We sorted the array upfront twice in $O(n\log(n))$ time. We divide the input repeatedly in half until we reached the base case. We then combined the results by finding the split pair and returning the pair with the minimum distance. So we have a recurrence that looks like this:

$$ \begin{align*} T(n) = aT(n/b) + n^c \\ T(n) = 2T(n/2) + n^c \end{align*} $$

The $c$ constant depends on the work we’re doing in each level. We first create the four arrays $left_x$, $left_y$, $right_x$ and $right_y$. This takes $O(n)$ time. We then find the split pair. If we find the split pair in $O(n^2)$ then $c = 2$ and by the master theorem, the total runtime is $O(n^2)$. This defeats the purpose since the naive solution runs in $O(n^2)$. We also know that we initially sorted the array in $O(n\log(n))$ so the final runtime is at least $O(n\log(n))$. So roughly we know that we need to find the split pair really fast in $O(n)$ to have $c = 1$ and therefore, keeping our runtime at $O(n\log(n))$.

Sorting $P_x$ by the x-coordinate and the y-coordinate $O(n)$ time

So we’re claiming that we’re sorting once only and then somehow we’re are repeatedly passing the two halfs of the $P_x$ sorted by the x-coordinate and by the y-coordinate. How?! For sorting by the x-coordinate, we simply split $P_x$ in half by calculating the median in $O(1)$ time and then iterating over $P_x$ to split the array into $left_x$ and $right_x$. That takes $O(n)$ time where $n$ is the current size of $P_x$.

Now that we have both $left_x$ and $right_x$. We want to create two arrays $left_y$ which is $left_x$ but sorted by the y-coordinate. We also want $right_y$ which is $right_x$ sorted by the y-coordinate. How do we do this in just $O(n)$ time? This is when we will use $P_y$! We will iterate over $P_y$ and if we see an element with an x-coordinate below or equal to the median then this element belongs to $left_y$ otherwise it belongs to $right_y$. Remember that $P_y$ is just $P_x$ but sorted by the y-coordinate. We are also assuming for the sake of simplicity that the points are distinct.

Finding the split pair in $$O(n)$$ time

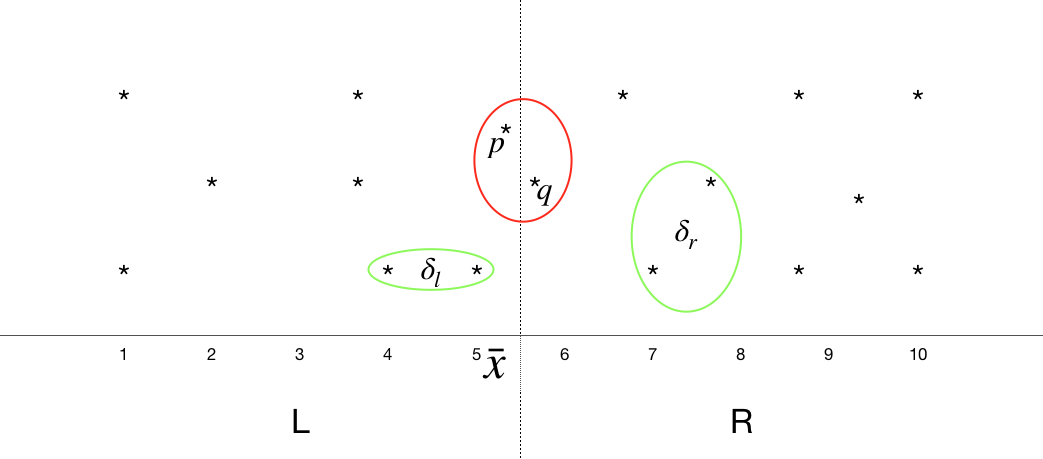Let’s assume that the minimum pair is not a left pair or a right pair and it is a split pair. In the algorithm we described above, let the left minimum distance be $\delta_l$ (shown above) and let the right minimum distance be $\delta_r$. Let $\delta$ be the minimum of $\delta_l$ and $\delta_r$. Also let the right most point in the left array be $\bar{x}$. Now construct $M$ to be an array with all the points that have x-coordinate between $\bar{x} - \delta$ and $\bar{x} + \delta$ sorted by their y-coordinate (we can use $P_y$ with a linear scan to insert any point that has an x-coordinate that fits our criteria). This linear scan costs $O(n)$ time which is fine by us!

Let $p=(x_1,y_1)$ and $q=(x_2,y_2)$ be the split pair points we’re trying to find where $p$ is in the left half and $q$ is in the right half. We claim the following:

Both $p$ and $q$ are in $M$.
At most 6 points are between $p$ and $q$ in M.

So, assuming the above is correct (we’ll prove it formally), we now have a constant number of pairs to look at. Basically, for each point, we will look at 7 points and therefore, we only have $7n$ pairs and so we can find the split pair in only $O(n)$ time!

But why why why the above is the correct? let’s look at the first claim.

Proof:
We want to show that if the closest pair of points is a split pair then our algorithm will find it. Since our algorithm only searches $M$, then we want to show that both $p$ and $q$ are in $M$. So assuming that $p$ and $q$ are the closest pair, we then know that $d(p,q) < \delta$. From here we can expand the euclidean distance definition:

$$ \begin{align*} \delta &> d(p,q) \\ &= \sqrt{(y_2-y_1)^2 + (x_2-x_1)^2} \\ &\geq \sqrt{\max\{(y_2-y_1)^2, (x_2-x_1)^2}\} \\ &= \max\{(y_2-y_1), (x_2-x_1)\} \end{align*} $$

This says that $p$ and $q$ must differ by less than $\delta$ in both their $x$ and $y$ coordinates!! So $|x_2-x_1| < \delta$. We also know that $p$ and $q$ are a split pair and so by definition we have $x_1 \leq \bar{x}$ and $x_2 > \bar{x}$. Therefore, we must have $x_1 \geq \bar{x} - \delta$ and $x_2 \leq \bar{x} + \delta$. Finally, since $M$ is defined to include all points such that the x-coordinate satisfies $\bar{x} - \delta \leq x \leq \bar{x} + \delta$ then $p$ and $q$ are in $M$ and thererfore, we will find them. $\blacksquare$

Let’s move to the second claim. why must we have 6 points only between $p$ and $q$?

Proof:
Without the loss of generality, assume that $q$ has the lower y-coordinate. We do know that both $p$’s x and y coordinates differ by less than $\delta$ from $q$’s x and y coordinates respectively. What do we know about the points between $p$ and $q$ in $M$?

Since $M$ is sorted by the y-coordinate, we do know that any point that comes between $p$ and $q$ must have a y-coordinate between $y_1$ and $y_2$. Since $y_1$ and $y_2$ differ by less than $\delta$, this makes the y-coordinate of any of these points be in between $y_2$ and $y_1 \leq y_2 + \delta$
We know that any point between $p$ and $q$ must have an x-coordinate between $\bar{x}-\delta$ and $\bar{x}+\delta$ by our construction of $M$.

Using the above restrictions, any point between $p$ and $q$ must be in one of the following boxes. (again, if you look at the x-axis, $M$ only allow points within $\delta$ of $\bar{x}$. If you look vertically, the fact that $M$ is sorted makes the points between $q$ and $p$ have a y-coordinate between $y_2$ and $y_1$ and that gap is also less than $\delta$!!).

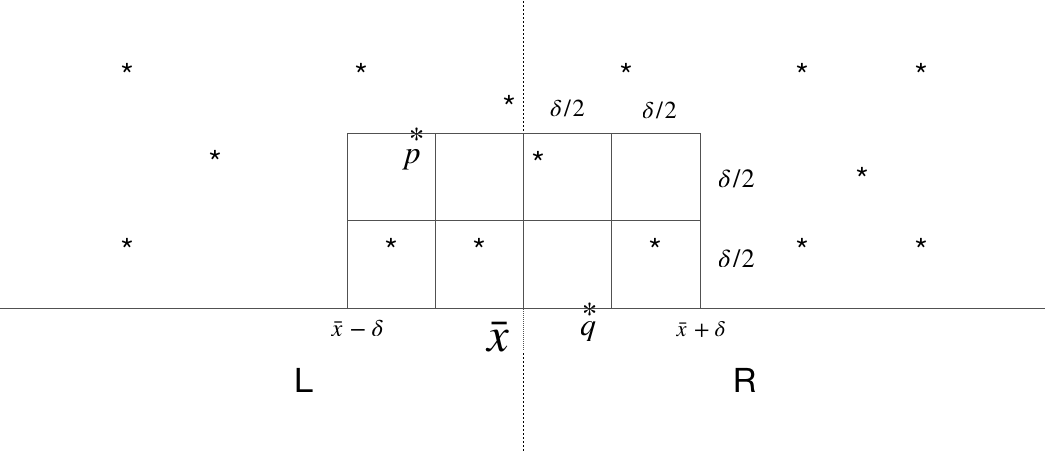
The next question is how many points do we have in each box?

We claim that each box has only 1 point. Proof: Suppose it doesn’t and some box in the diagram above has 2 points. Let these points be $a$ and $b$. This means than $a$ and $b$ are both a left pair or a right pair. Moreover, the distance between $a$ and $b$ is at most $\sqrt{(\delta/2)^2 + (\delta/2)^2} = \delta/\sqrt{2} < \delta$. This is a contradiction, since by assumption we said both $\delta_l$ and $\delta_r$ are greater than $\delta$. Therefore, we must have 1 point in each box and so there are only 6 points between $p$ and $q$. $\blacksquare$ Wonderful!!

References

These are my study notes from chapter 3 of Algorithms Illuminated: Part 1: The Basics. Buy this book!!!