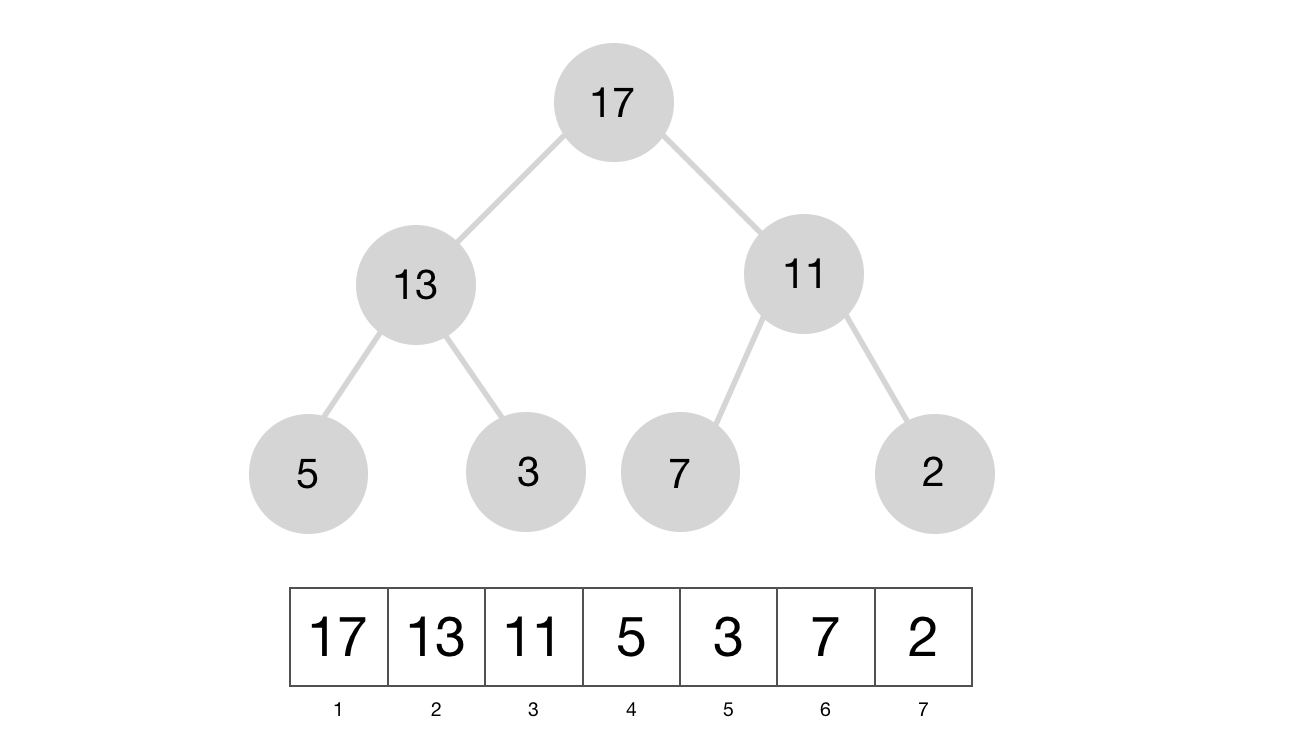
The heap data structure is an array \(A\) that can be viewed as an almost complete binary tree. Each node in the tree is represented by an element in the array. \(A[1]\) is the root of the tree. In the above tree, \(A[1]=17\) is the root of the tree.

Because the heap is based on a complete binary tree, the height of a heap of \(n\) elements is \(\Theta(\log(n))\). As a reminder, the height of a node is the longest path down from the node to a leaf and the height of the tree is the height of the root of the tree. This observation is crucial in proving that many operations on heaps run in \(O(\log(n))\) time.

Finding the Parent, Left and Right Children

Given an element \(A[i]\). Its parent is located at \(A[\lfloor i/2 \rfloor]\). For example the parent of 2 (index 7) is \(A[\lfloor 7/2 \rfloor]=A[3]=11\). The left child is \(A[2*i]\) and the right child is \(A[2*i+1]\). For example the right child of 13 (index 2) is \(A[2*2 + 1] = A[5] = 3\).

int parent(i) {
    return i/2; // we know that i/2 is rounded down so we don't need to floor
}
int left(i) {
    return i << 1; // 2*i;
}
int right(i) {
    return (i << 1) + 1; // 2*i+1
}


The Heap Property

There are two kinds of binary heaps, min heaps and max heaps. Depending on the heap type the array must satisfy a heap property. The heap property depends on the type of the heap. For any given element \(A[i]\) we must have:

If this is a max-heap then,

\(A[parent(i)] \geq A[i]\)

If this is a min-heap then,

\(A[parent(i)] \leq A[i]\)

The heap property is crucial. Because of it, we know that the root of the heap must be the smallest or the largest element in the heap and therefore, extracting the minimum or the maximum depending on the heap type can be done in constant time!

Maintaining the Max-Heap Property

Suppose we have an element \(A[i]\) that is smaller than its children. This is a violation of the max-heap property, how do we fix this? First we will assume that both children of \(A[i]\) maintain the heap property. We know in constant time that the children are \(A[2*i]\) and \(A[2*i+1]\). We can then swap \(A[i]\) with the larger of the two children. Finally, we recursively call the function on the larger child we just swapped at \(A[i]\). Let’s look at a simple implementation:

void max_heapify(int i) {
    int l = left(i);
    int r = right(i);
    // (1) check if the left child is greater
    int largest = i;
    if (l <= length && A[l] > A[i]) {
        largest = l;
    } else {
        largest = i;
    }
    // (2) check if the right child is greater
    if (r <= length && A[r] > A[largest]) {
        largest = r;
    }
    // if one of the children is greater, swap it
    // with i and then call heapify again on the child
    // we swapped with
    if (largest != i) {
        std::swap(A[i], A[largest]);
        max_heapify(largest);
    }
}

How long does max_heapify take? Well, in the worst case, we will go down all the way to a leaf and so the runtime is \(O(h)\) which is \(O(log(n))\).

Building a Max Heap

Based on how we store the heap elements in the array, the leaves of the tree are located stating at \(A[n/2+1], A[n/2+2],...,n\). (proof?). Therefore, if we go over the remaining nodes in the tree and ran max-heapify, it will be enough to gaurantee that every element of \(A\) maintains the heap property. Therefore, we can use the following to build a max-heap:

void build_max_heap(A) {
    for (int i = A.length/2; i >=1; i--) {
        max_heapify(A, i);
    }
}


Example

Let’s look at an example of building a max-heap using the above idea. We’re given the following array and we want to build a max-heap out of it.

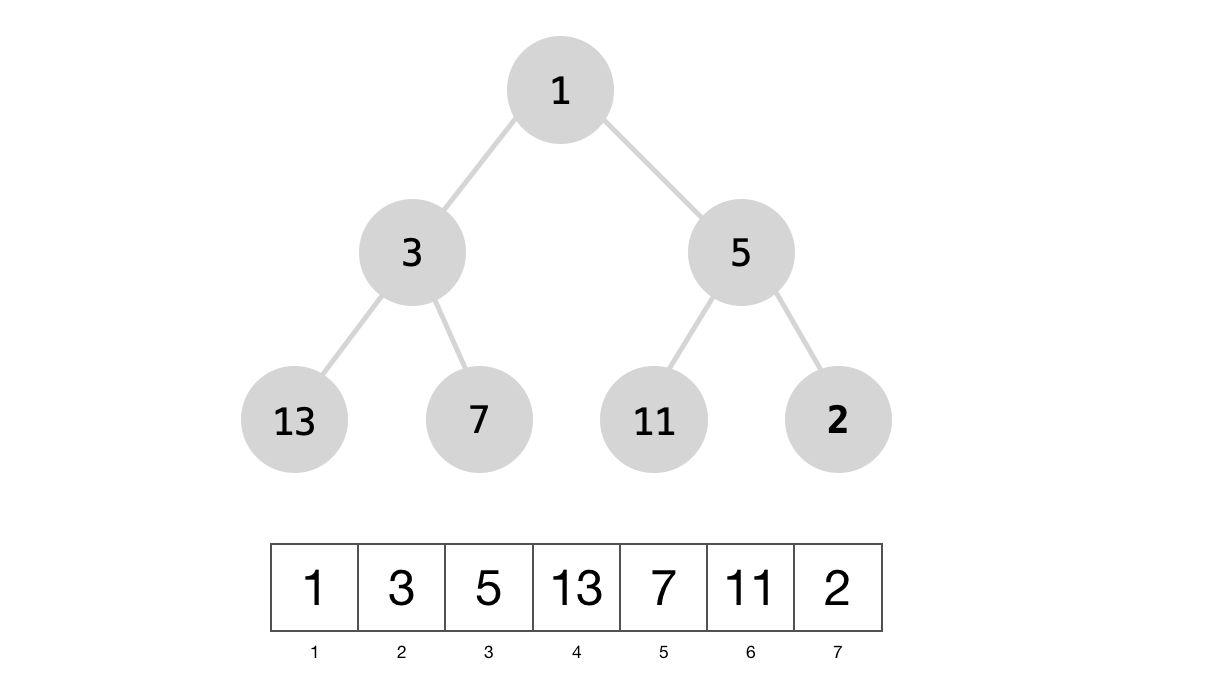
To build a max-heap we’ll only consider the non-leaf nodes, highlighted below.
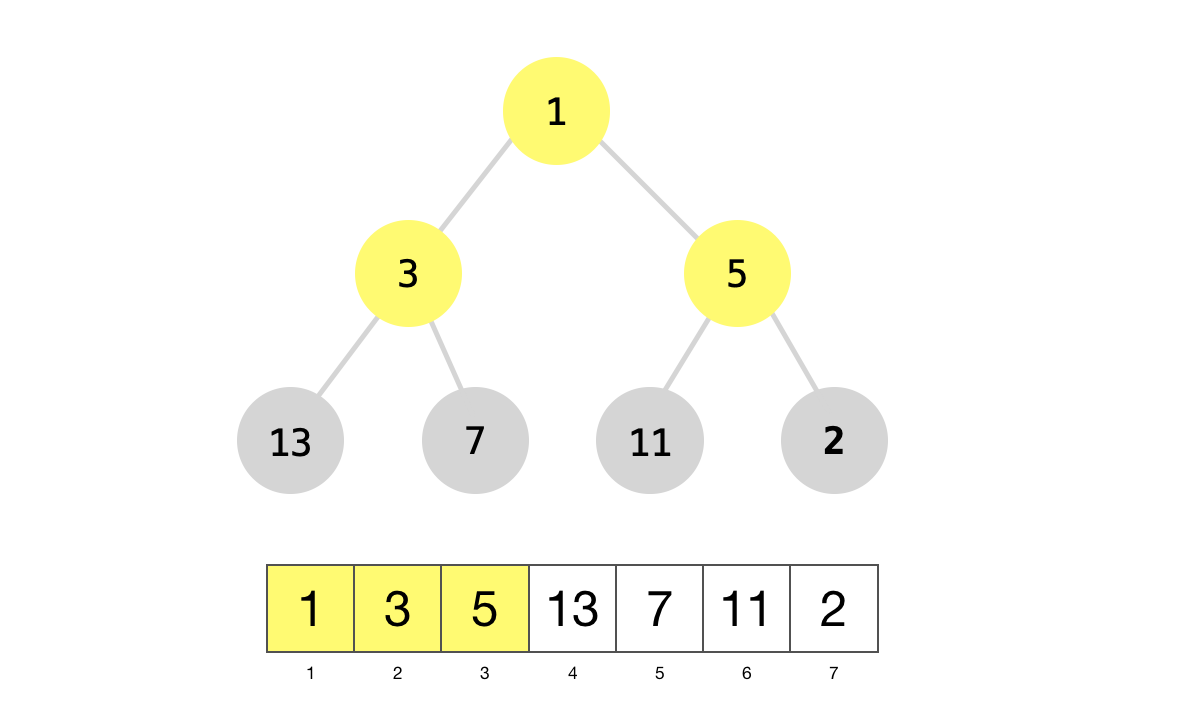
We’ll start with node 5 and call max_heapify on it. In max_heapify, we’ll swap both nodes 5 and 11. We will then recusively call max_heapify node 5.
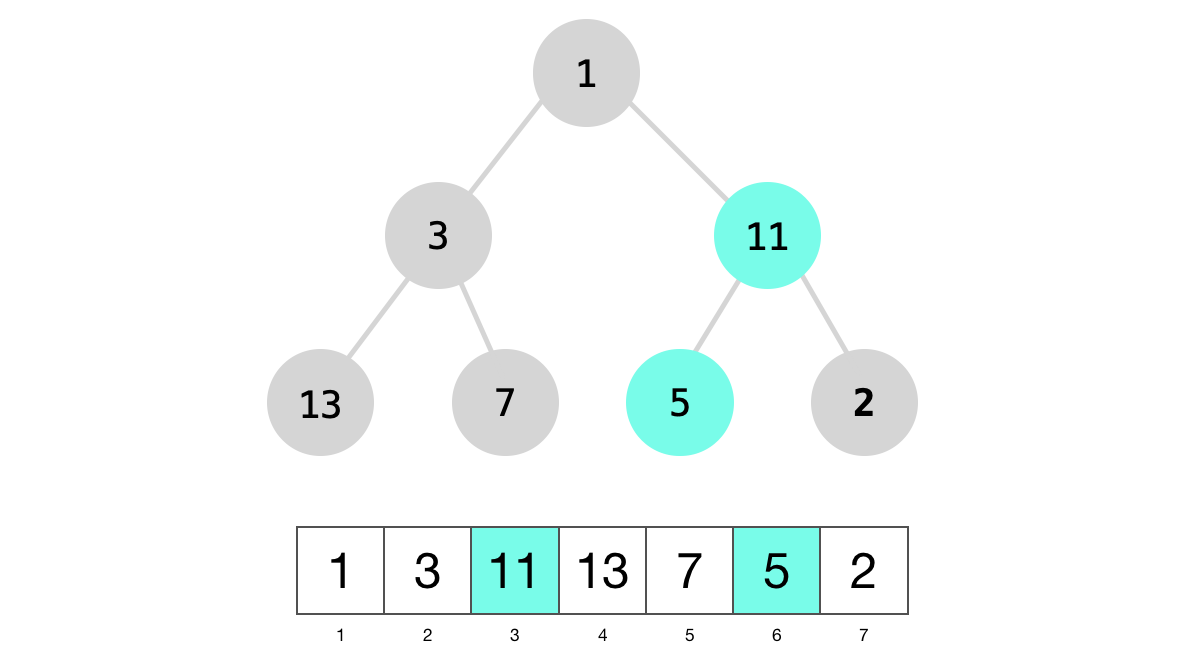
Notice that node 5 is now a leaf node so we can’t push it further down the tree and so we’ll move to the next node, node 3.
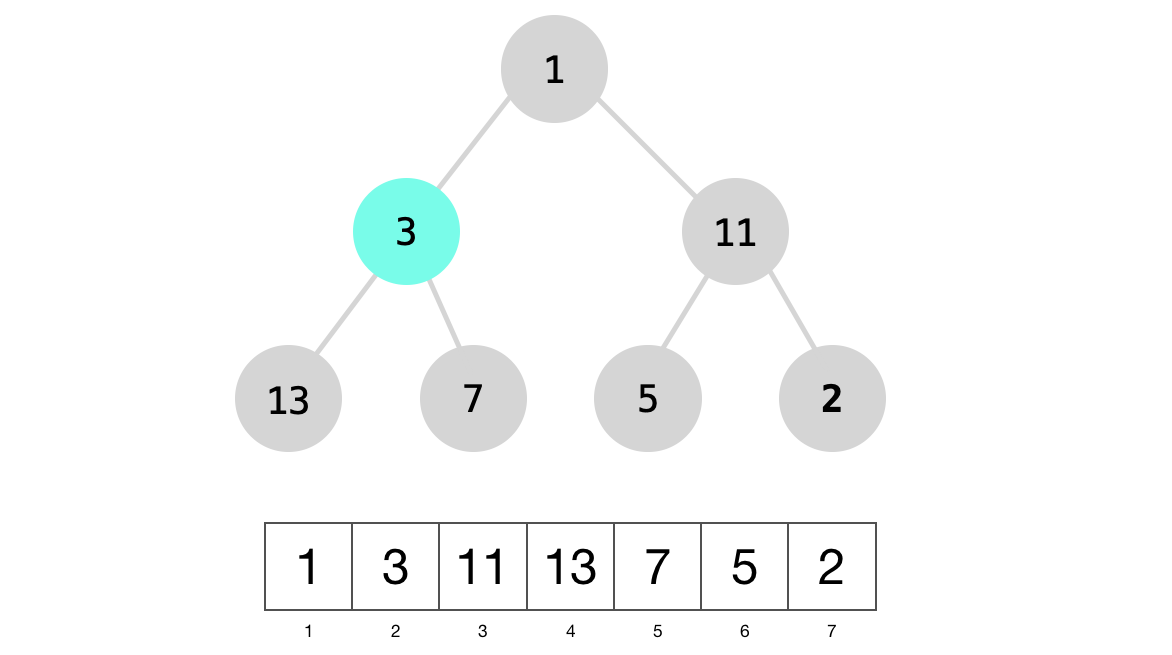
Node 3 above will be swapped with the larger of its children, node 13.
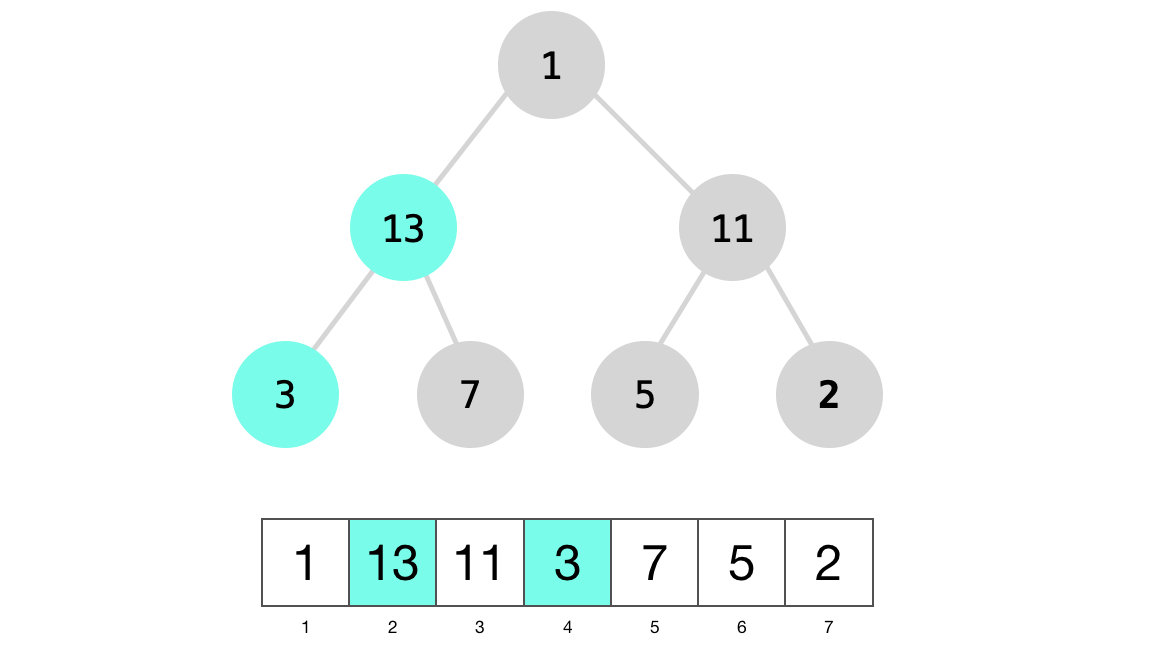
Notice how nodes 3 and 13 are now swapped. Next we will recursively call max_heapify on node 3 but node 3 is a just a leaf node and we will stop. The final node in the build_max_heap for loop is node 1.
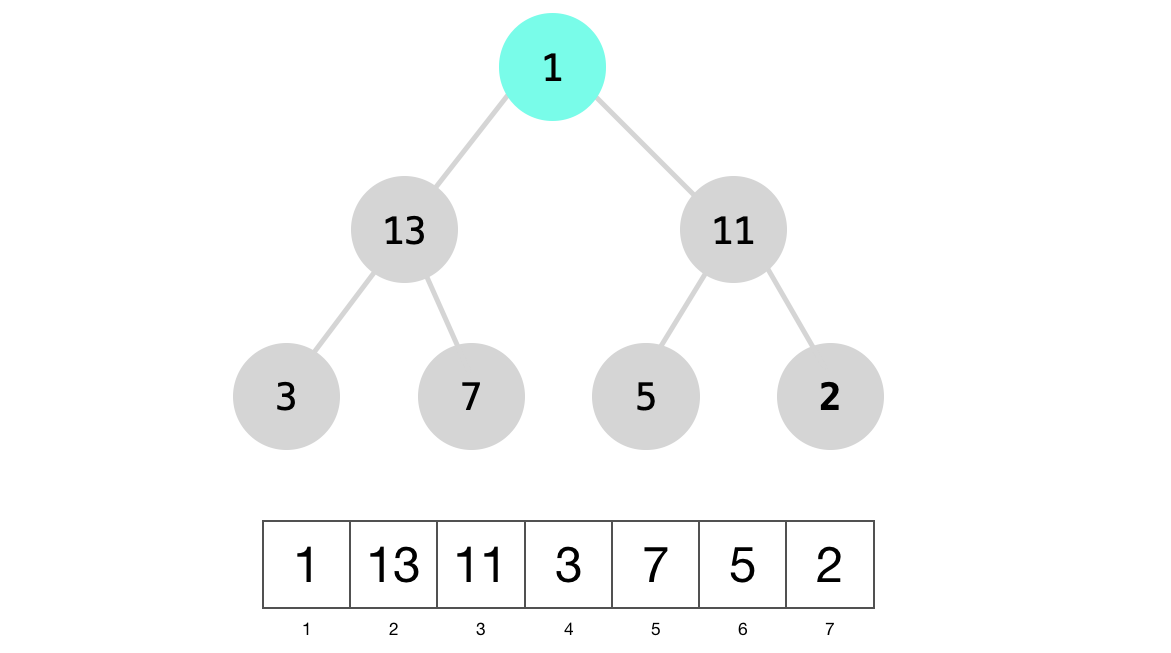
We will swap node 1 with the larger of its children, node 13. 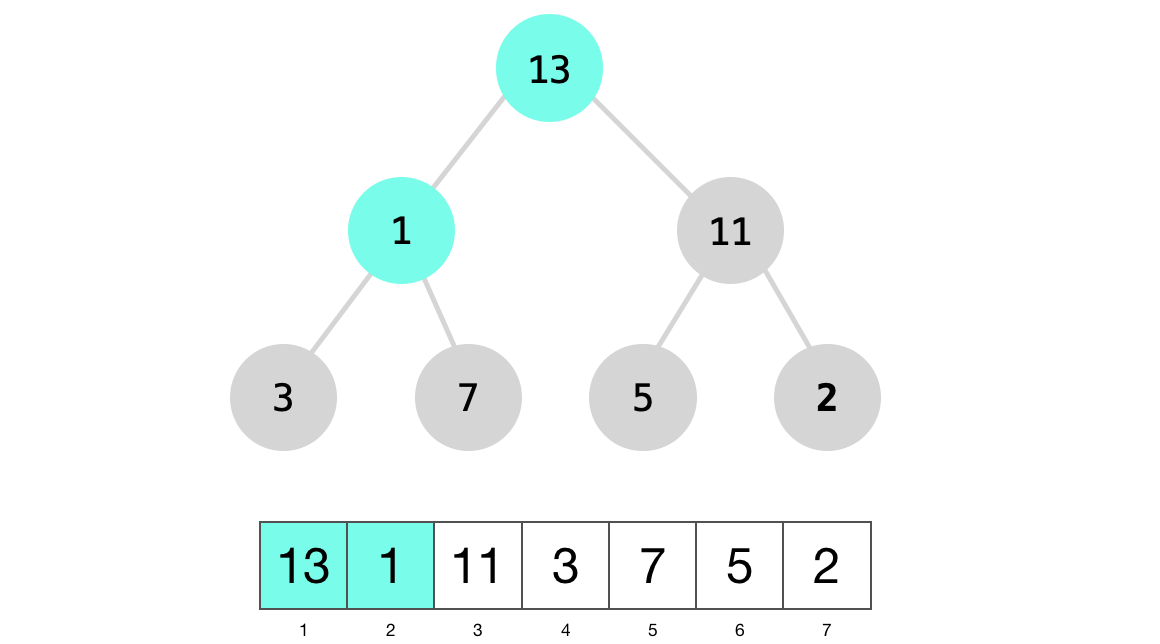We will then recusively call max_heapify on node 1. 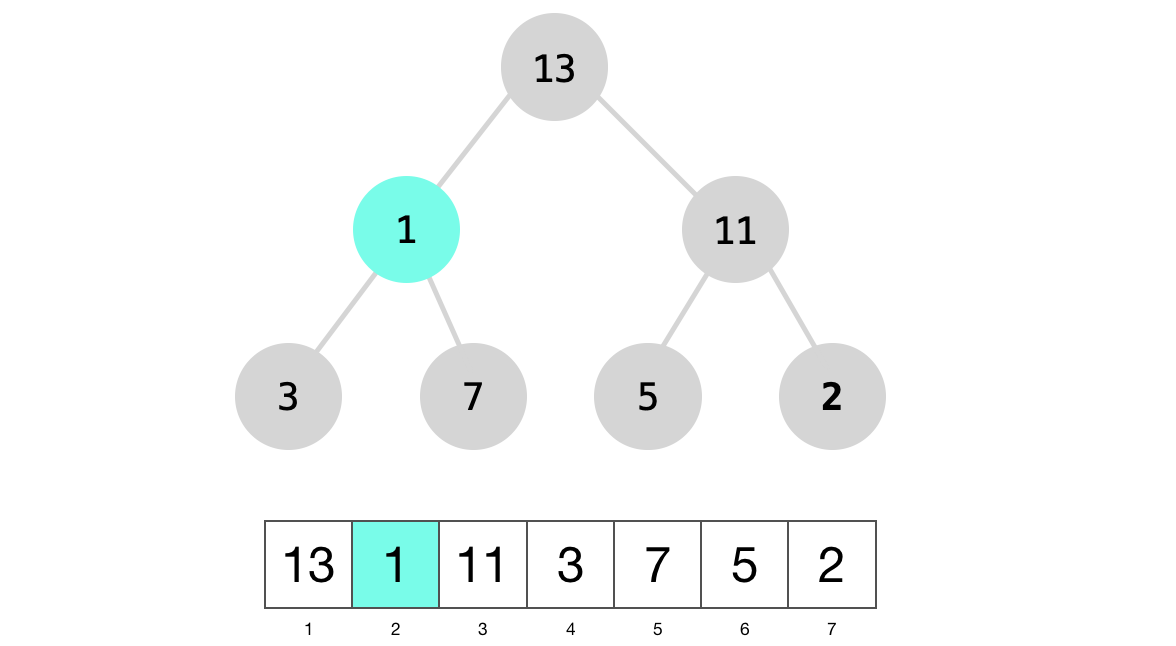And finally we will swap 1 with the larger of its children, node 7.
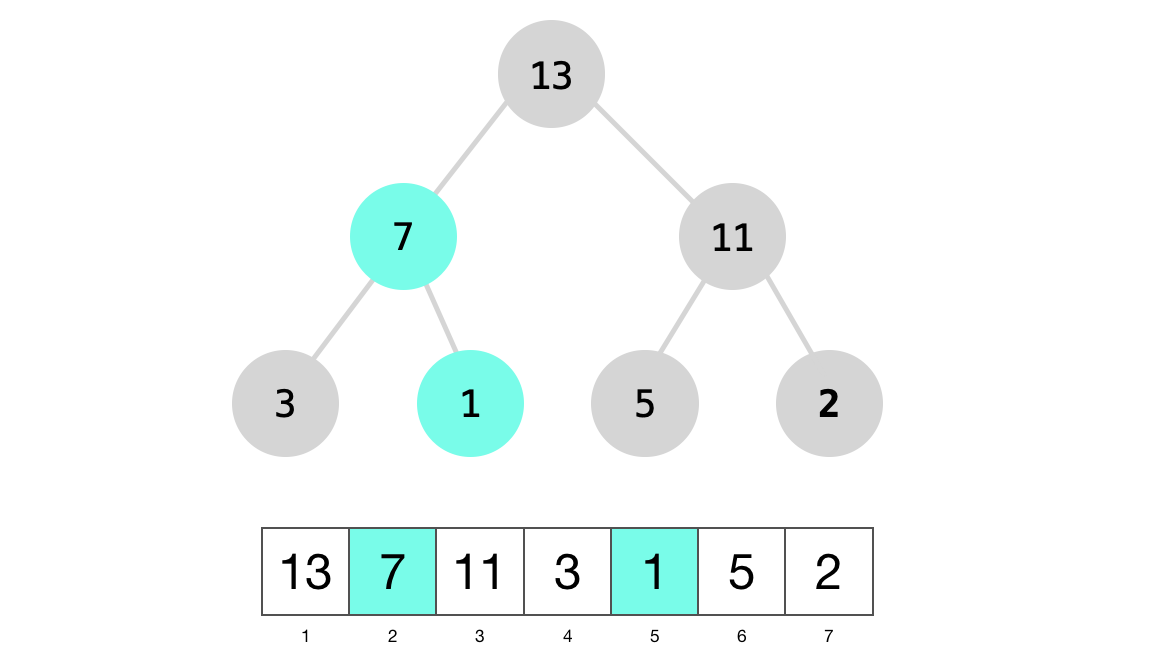
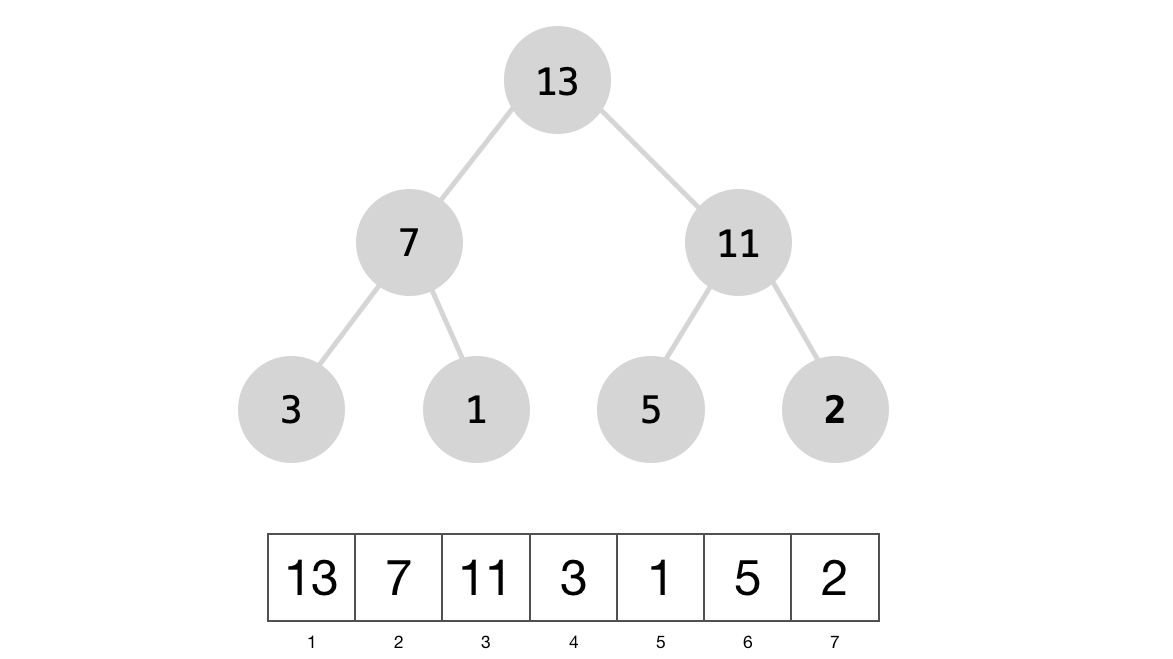
Finally, you can see now that the tree/array is a max-heap:

Correctness Proof

Why should we believe that build_max_heap works? This is going to be exactly what’s in CLRS (my notes for myself to quickly remember). We’ll show that it works by proving that the following loop invariant is maintained prior to the first iteration, before each iteration and when the loop terminates.

At the start of each iteration of the for loop in build_max_heap, each node \(i+1, i+2, ..., n\) is the root of a max_heap.

Initialization: Before the first iteration that starts at \(A[\lfloor n/2 \rfloor]\), the nodes \(A[\lfloor n/2 \rfloor + 1], A[\lfloor n/2 \rfloor + 2],...A[n]\) are leaf nodes and therefore each node is a root of a max-heap.

Maintenance: (so the gist here is that max_heapify will maintain that node \(i\) follows the heap property because indices \(2*i, 2*i+1\) are higher than \(i\) and therefore already maintain the heap property).
At each iteration, we call max-heapify on the node \(A[i]\). The children of node \(A[i]\) are \(A[2*i]\) and \(A[2*i+1]\). Since they both have a higher index than \(i\) then this means that both of these nodes are already roots of max-heaps by the loop invariant. Recall that max_heapify requires that the children maintain the heap property. Also we know that max_heapify maintains the heap property for any nodes to follow \(i+1, i+2, ..., n\). Therefore, when we decrement \(i\), the loop invariant will be established before the next iteration.

Termination: At termination when \(i=0\), we know by the loop invariant that the nodes \(1, 2,...,n\) are all roots of max-heaps, specifically node \(1\) which is the root of the final max heap we have. So we are done.

I would obviously recommend looking at CLRS’s way unless I’m in a rush and this is easily accessible on my phone.

Running Time

The most exciting question is how long does it take to build a max heap? We know that max_heapify takes \(O(\log(n))\) time for each node. We also know that we at most have \(O(n)\) iterations. This means that building a max heap will run in \(O(n\log(n))\). But we derive a much tighter bound than this by observing that:

(1) Binary heaps with \(n\) nodes have height \(\lfloor \log(n) \rfloor\).
(2) At any height \(i\), we have at most \(\lceil \frac{n}{2^{i+1}} \rceil\) nodes.


Aside: What does (2) mean? Suppose we have a binary heap with \(n=7\) just like the tree below: 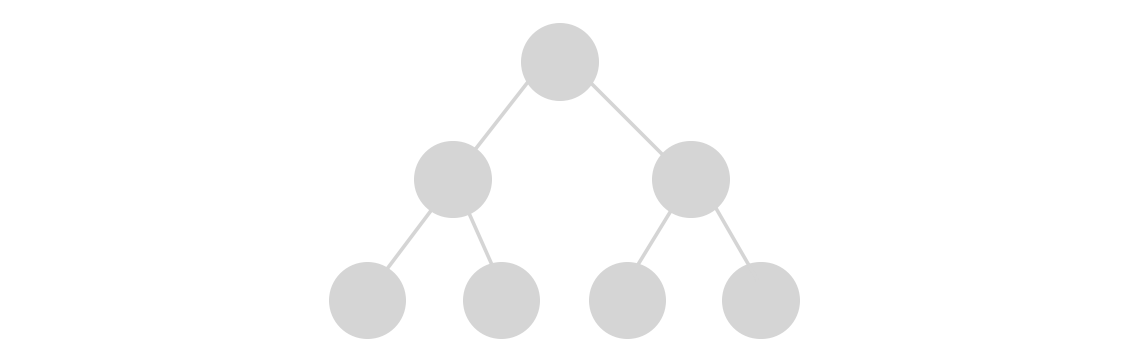The number of nodes at height 0 (leaves) is \(\lceil \frac{n}{2^{i+1}} \rceil = \lceil \frac{7}{2^{0+1}} \rceil = \lceil 3.5 \rceil = 4\)
The number of nodes at height 1 is \(\lceil \frac{7}{2^{2}} \rceil= 2\)
The number of nodes at height 2 (root) is \(\lceil \frac{7}{2^{3}} \rceil= 1\)
Formal Proof:
TODO


We can now sum the work we’re doing at each level which is just the height of the level multipled by the number of nodes in that level. We do that for each level in the tree, from the 0th level to the \(\lfloor \log(n) \rfloor\)’s level:

$$ \begin{align*} \sum_{i=0}^{\lfloor \log(n) \rfloor} \lceil \frac{n}{2^{i+1}} \rceil O(i) = O(n\sum_{i=0}^{\lfloor \log(n) \rfloor} \frac{i}{2^{i}} ) \end{align*} $$

We can use the following summation:

$$ \begin{align*} \sum_{k=0}^{\infty} kx^k = \frac{x}{(1-x)^2} \end{align*} $$

By substituting \(x\) with \(1/2\) to get:

$$ \begin{align*} \sum_{k=0}^{\infty} \frac{k}{2^k} = \frac{1/2}{(1-1/2)^2} = \frac{1}{2(1/4)} = 2 \end{align*} $$

And therefore, we can bound the earlier summation to just:

$$ \begin{align*} O(n\sum_{i=0}^{\lfloor \log(n) \rfloor} \frac{i}{2^{i}} ) = O(n) \end{align*} $$

and we’re done!

Heapsort


TODO

References

These are my study notes / summary on chapter 6 in CLRS.