my photo We are given a graph \(G = (V,E)\) and we want to know if there exists a cycle in \(G\).

Undirected Graphs

This is extremely simple. We already keep track of nodes visited so far. If it happens during our search that we come across a visited node then we’re done! there must exists a cycle otherwise, we won’t ever re-visit any vertex in \(G\).

bool bfs(int start, std::vector<std::vector<int>>& graph) {
    std::queue<int> q;
    q.push(start);
    std::vector<int> visited(graph.size(), false);
    visited[start] = true;
    while (!q.empty()) {
        int v = q.front();
        q.pop();
        for (int i = 0; i < graph[v].size(); i++) {
            int u = graph[v][i];
            if (visited[u] == false) {
                q.push(u);
                visited[u] = true;
            } else {
                // CYCLE
                return true;
            }
        }
    }
    return false;
}

Directed Graphs

Suppose we apply the earlier idea used in undirected graphs. We traverse the nodes and if we see a node we’ve seen before, we conclude that we found a cycle. Let’s take the graph above and start a DFS pass from the node \(a\) below:

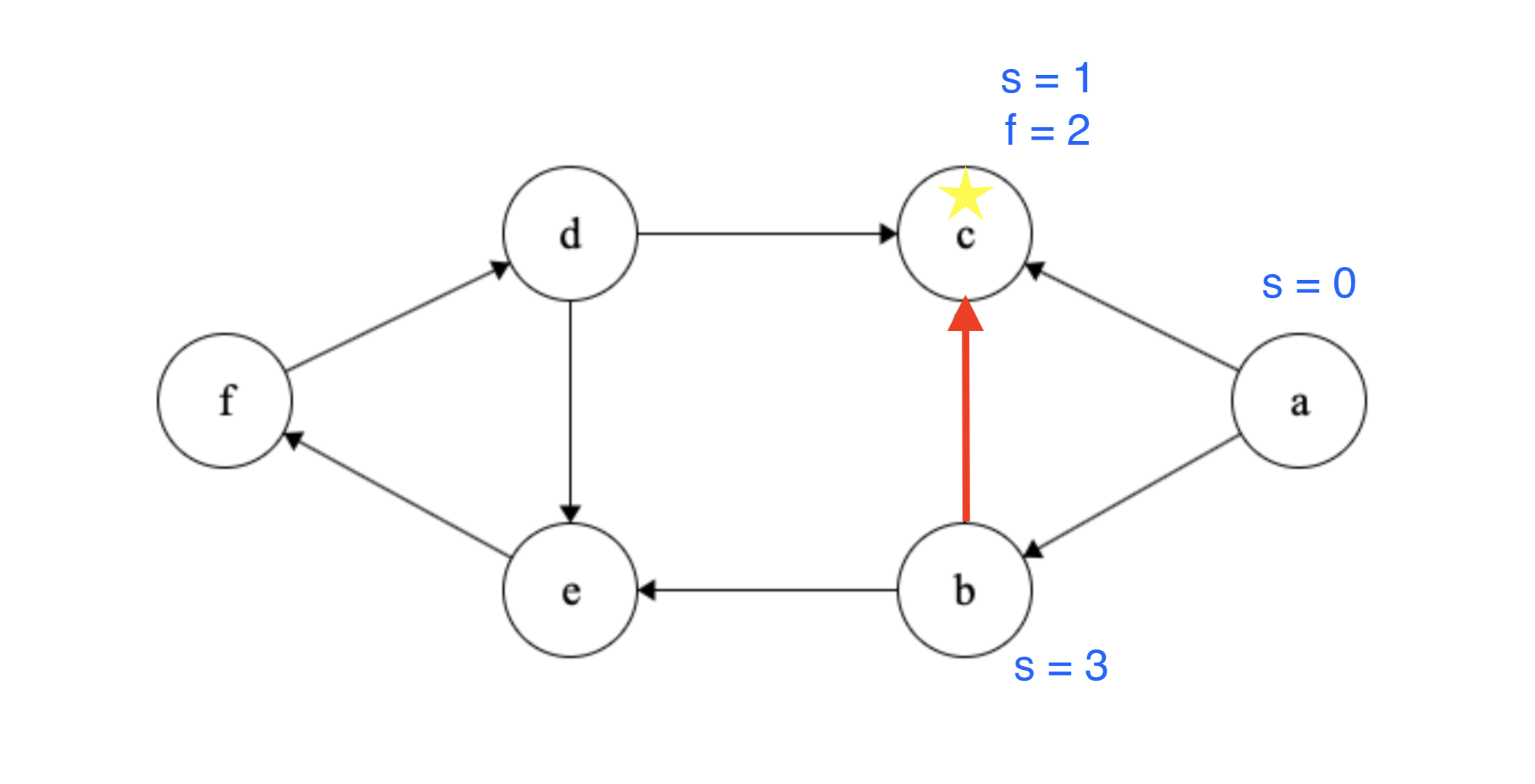
my photo

From \(a\) we visit \(c\). Node \(c\) doesn’t have neighbors so we mark its finish time and then we go back to \(a\). We next visit \(b\) and mark its start time. From \(b\), we see \(c\) again! is this a cycle? NO. The idea fails here.

In directed graph we instead have three types of nodes.

A node that hasn’t been discovered yet (we didn’t mark its start time yet). Node \(e\) is one example above. Let’s color this node black.
A node that has been discovered (we marked its start time) but it hasn’t been processed yet (we didn’t mark its finish time). Let’s color this node gray.
A node that has been processed. We marked its start time and its finish time. Let’s color this node white.

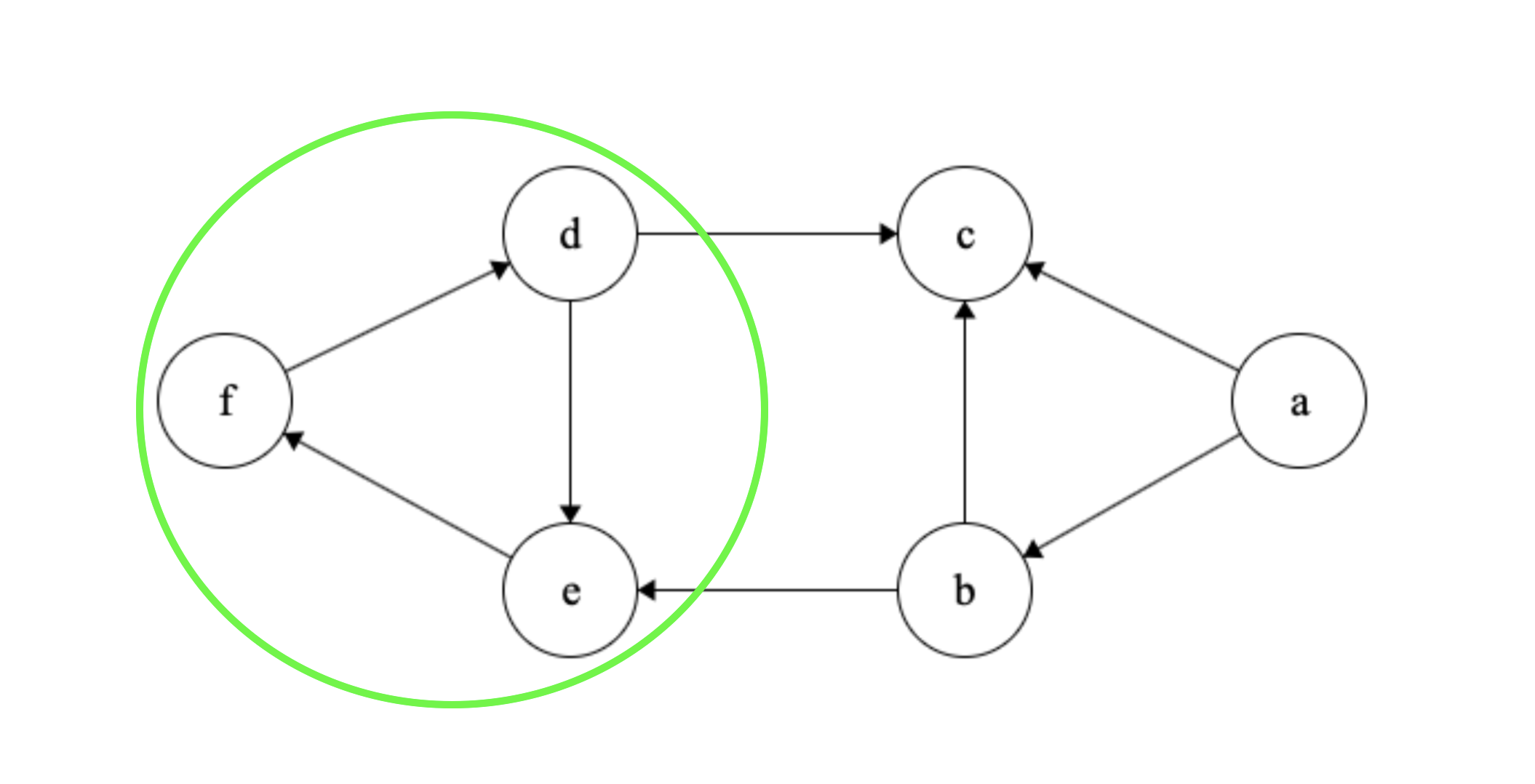
When will a directed cycle happen? when we re-discover a gray node! below is a continuation of the traversal that started from node \(a\). We discover nodes \(b, e, f\) and \(d\). From \(d\) we re-discover \(e\) but \(e\) has already been discovered because it’s gray! This means we have a cycle.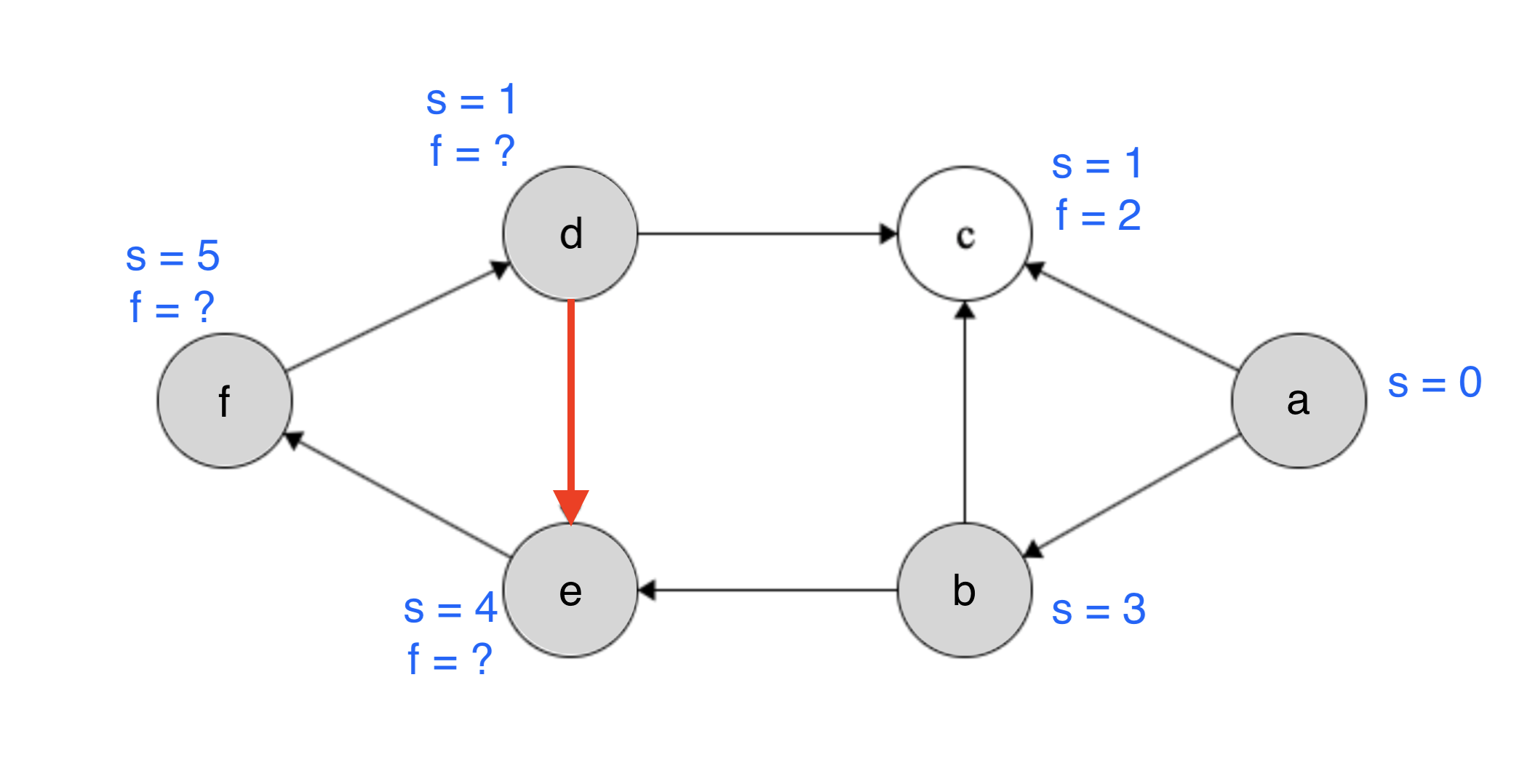

The following code implements this idea which is just a small modification to a typical depth search first traversal.

void dfs(graph& g, int v, int *color) {
    color[v] = gray;
    for (auto i = 0; i < g[v].size(); i++) {
        int u = g[v][i];
        if (color[u] == white) {
            dfs(g, u, color);
        } else if (color[u] == gray) {
            // CYCLE
        }
    }
    // we are done with the node for good
    color[v] = black;
}

Correctness Proof

TODO

Implementation

https://github.com/strncat/algorithms-and-data-structures/tree/master/graphs/cycles

References

CLRS