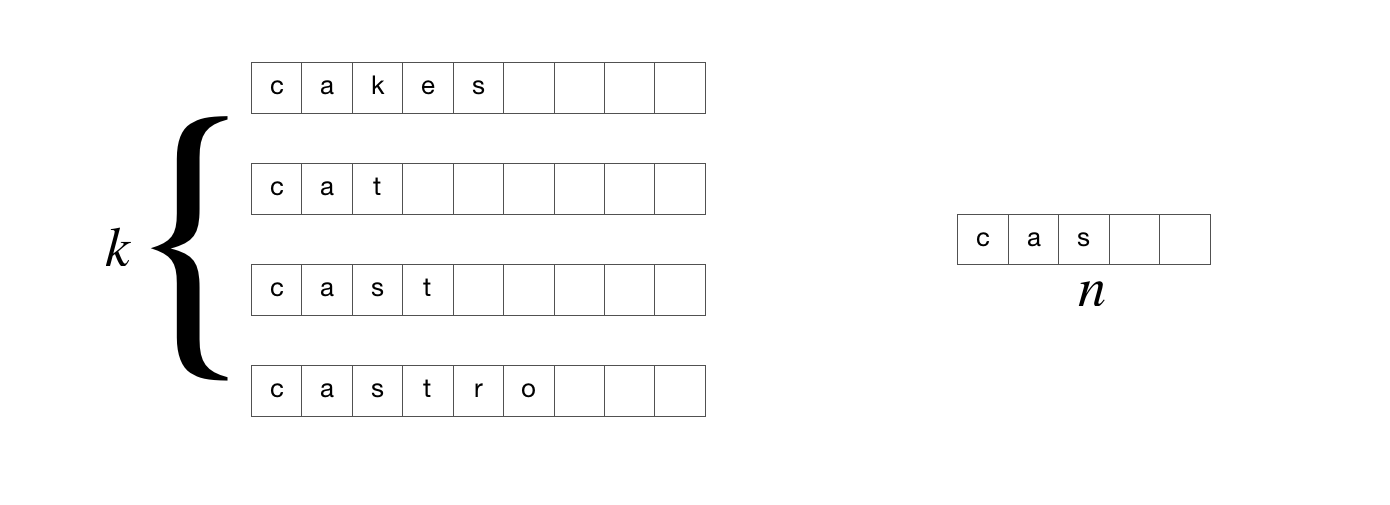
Given a set of \(k\) strings of total length \(m\) and a prefix \(p\) of length \(n\), we want to find all the strings that start with \(p\). The simplest solution would be to match each of the \(k\) strings with the prefix. This will take \(O(m)\) time. However, suppose that we now we have \(r\) patterns, then this approach will take \(O(mr)\) time which is really slow. Similar to the RMQ notation, we will write \(\langle O(1), O(mr)\rangle\) where \(O(1)\) is the preprocessing time and \(O(mr)\) is the query time. How can we make it faster?

The Trie Data Structure


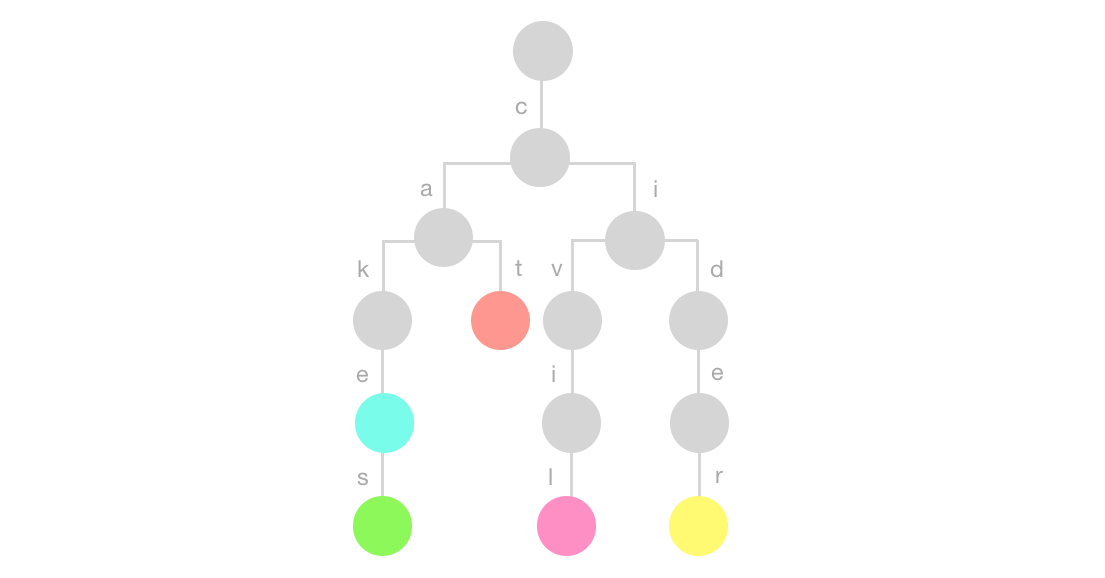
The trie (pronounced “try”) data structure is an efficient data structure that can help us achieve a faster running time when searching for prefixes. In the picture above forexample, we can find the words that start with the prefix “ca” by starting at the root and traversing down to find the words (words end with colored nodes): cake, cakes and cat.

Here are some important properties of tries

  • Each node indicates whether it is the end of a valid word or not. In the above example, colored nodes represent the end of valid words. We can simply use a bool value (yes/no) in each node to do this.
  • Each node will have \(R\) children/edges where \(R\) is the alphabet size.
  • Edges represent letters. For example, the root node has one edge (\(c\)) to the nodes below.
  • Each node also has only one parent.

    Let’s look at what a trie really looks like:
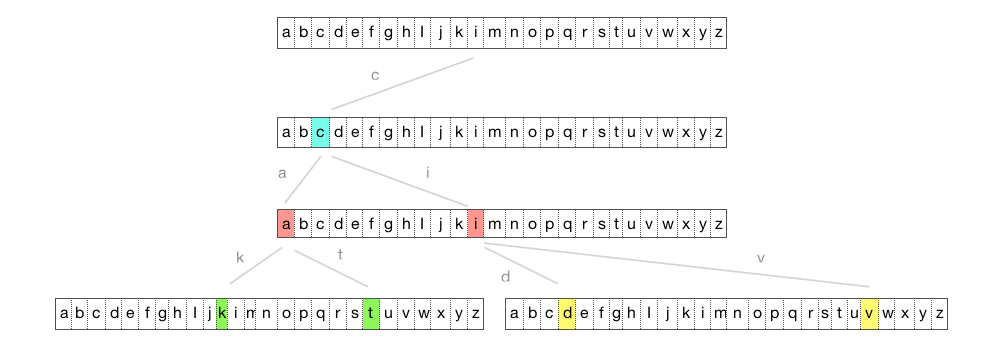    You can see above, the root has only one edge of value \(c\). From \(c\), we can traverse to either \(a\) or \(i\). From \(a\) we can traverse to \(k\) or \(t\). From \(i\) we can traverse to \(d\) or \(v\) and so on.

Node and Edges Representation

This can be done in many ways. The following is just one way that uses a struct to represent a node. This struct will include a bool value to indicate whether we have arrived at a valid word or not. Each node/struct will also have an array to store all possible edges. Each array position holds a pointer to a node struct, intially all set to NULL. Here, we will consider the English alphabet which consists of 26 letters. We will use position 0 to represent ‘a’, 1 to represent ‘b’ and so. We will take advantage of the fact that the ASCII value for the letter a is 97 and z is 122 and so to store ‘c’, we simply find the right position in the array by subtracting ‘a’ (97) from ‘c’ (99) to get 2 which is the correct position for ‘c’.

#define SIZE 26
typedef struct node {
    bool marker; // this is to indicate if it's the end of a valid word
    int value; // we'll use this to keep track of the number of possible matches at this node
    struct node *children[SIZE] = {NULL}; // 26 possible edges, edges represent letters in a trie
} node;
// a trie consists of a a root node and that's about it
typedef struct trie {
    node *root;
    trie() {
        root = new node();
    }


Prefix Search

Given a prefix \(p\) of length \(n\), we want to output all the possible words that start with \(p\). To do, we start with the root of the trie and the first letter of \(p\). We then check if the root contains a non-null node at the first letter of \(p\). If there is, then we move to this new node and advance to the next letter of \(p\). We repeat the same process until we either exit (return NULL) or reach the last letter of \(p\) and return that node. 

// return NULL if the pattern doesn't exist, otherwise 
// return the node we reached last (should be the pattern's last letter)
node* find_prefix(std::string pattern) {
    long m = word.length();
    node *current = root;
    // search for word in the tree rooted at root
    for (int i = 0; i < m; i++) {
        // find the correct location for letter word[i]
        int index = word[i] - 'a';
        if (!current->children[index]) { // null pointer
            return NULL; // not found
        }
        // follow that link
        current = current->children[index];
    }
    return current;
}

Once we find the prefix (node returned above is not null), we know that all the words in the current subtree are words that start with prefix. To collect all these words, we pass a queue or any container of our choice to collect below. collect is just a depth first search that recursively traverses the subtree rooted at current. 

// collect matches recursively from all branches
// save them in q
void collect(node *current, std::string prefix,
    std::queue<std::string> &q) {
    if (current == NULL) { return; }
    if (current->marker) {
        q.push(prefix);
    }
    for (int i = 0; i < SIZE; i++) {
        if (current->children[i] != NULL) {
            char c = i + 'a';
            collect(current->children[i], prefix + c, q);
        }
    }
}

Finally, we utilize find_prefix to find the prefix and then, pass a queue to collect which will fill the queue with all matches. 

// prefix match: print all possible matches
int words_with_prefix(std::string prefix) {
    node *current = search(prefix);
    if (current == NULL) { // no matches
		return 0; 
	}
    // right now, current has the last letter of the prefix
    // any valid word that comes after is a possible match 
    // we want to return all of them, we use a queue for that
    std::queue<std::string> q;
    collect(current, prefix, q);
    while (!q.empty()) {
        printf("%s\n", q.front().c_str());
        q.pop();
    }
    return current->value; // total matches
}

Insert

Suppose we want to insert a new word of length $n$. We follow a similar process. We start at the root and we also start at the beginning of the word to be inserted. If the letter we’re on has already a link in the root then we follow it a long and move to the next letter as well. If the link is null then we create a new node for that letter. 

void insert(std::string word) {
    if (search(word)) { // word exists
        return;
    }
    int length = (int) word.length();
    node *current = root;
    current->value++; // increment word count
    for (int i = 0; i < length; i++) {
        int index = word[i] - 'a';
        if (!current->children[index]) {
             // this letter doesn't exist, create it
            current->children[index] = new node();
        }
        // this letter has a link already, follow it along
        current = current->children[index];
        current->value++;
    }
    // mark the last node, this is the end of our word
    // this is a marker of an end to a valid word
    current->marker = true;
}

insert takes \(O(n)\) which is the length of word.

Delete

To be added.

Longest Prefix

To be added

Running Time

We mentioned above that insert and search both take \(O(n)\) time where \(n\) is the length of the pattern. How long does it take to build a trie to represent all words of total length \(m\)? We need to make \(k\) insertions each of which will take \(O(\)size of each word\()\). Since the total length of all words is \(m\), then the total time is \(O(m)\) which happens only once initially. Therefore, in the RMQ notation we will have \(\langle O(m), O(n) \rangle\) which is a lot better than the naive solution.

Full Implementation

https://github.com/strncat/algorithms-and-data-structures/tree/master/strings/trie.cpp

References

  • Algorithms by Robert Sedgwick and Kevin Wayne
  • http://web.stanford.edu/class/cs166/