Depth first search like breadth first search is an algorithm used to explore a graph. Let \(G = (V, E)\) be a graph consisting of \(V\) vertices and \(E\) edges and let \(s\) be the source vertex where we will start the traversal from. Depth first search explores the graph from the root as deep as possible until there are no more vertices to visit and then resumes the search again from a different branch.
In a depth first search, we typically keep track of the time we first discovered a vertex and also the time we finished processing a vertex (after we look at all of its neighbors). This information will help later in topologically sorting a graph.
Implementation Details
To perform a depth first search, we will maintain the following data structures:
- A set or an array that keeps track of the visited nodes. Remember that \(G\) might contain cycles and so we want to make sure that we explore each node once.
- A stack. We want to explore the nodes closest to \(s\) first. Since we’re insterested in going as deep as possible, a stack will be the ideal data structures. Note that we can just eliminate the use of an explicit stack by using recursion (implicit stack) as we’ll be doing in the implementation below.
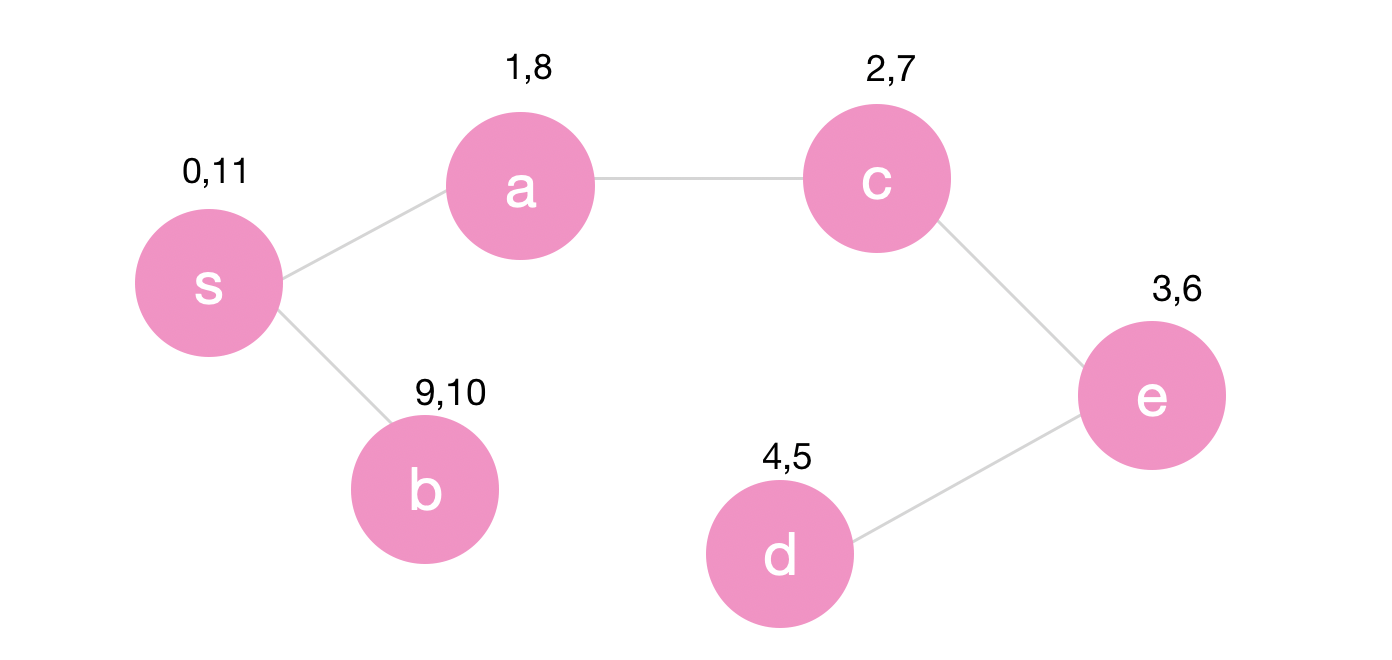
Example
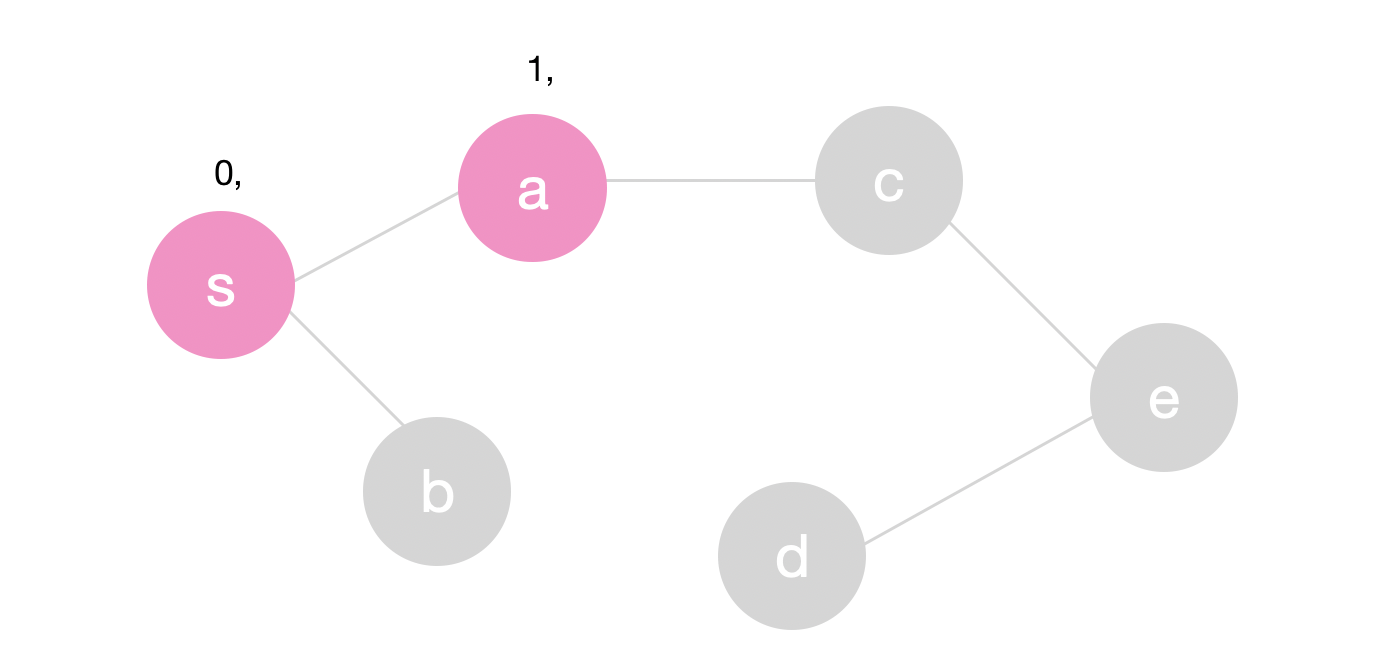
Let’s explore the graph above. We will start from \(s\) and as soon as we see \(a\) we’ll recursively call dfs again. The start time for \(s\) is 0 and the start time for \(a\) is 1.
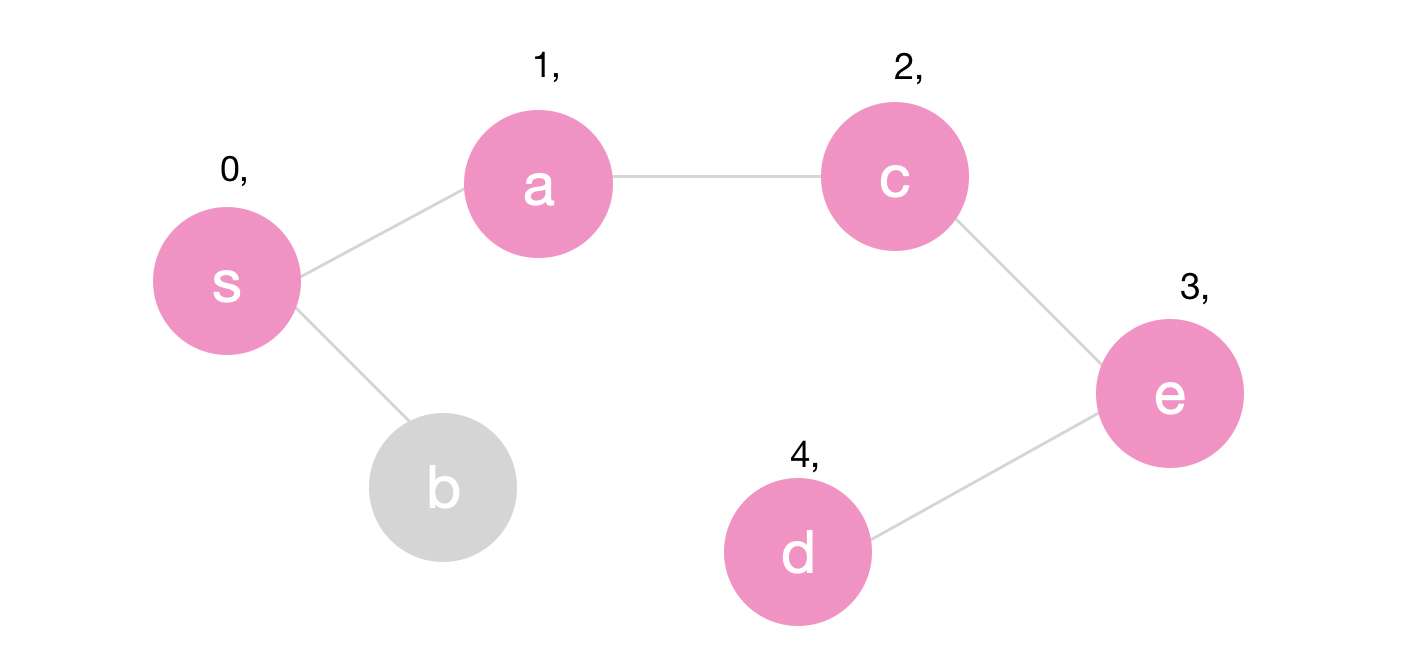
Next we will recursively visit \(c\), \(e\) and \(d\). They will have start times 2, 3 and 4 respectively.
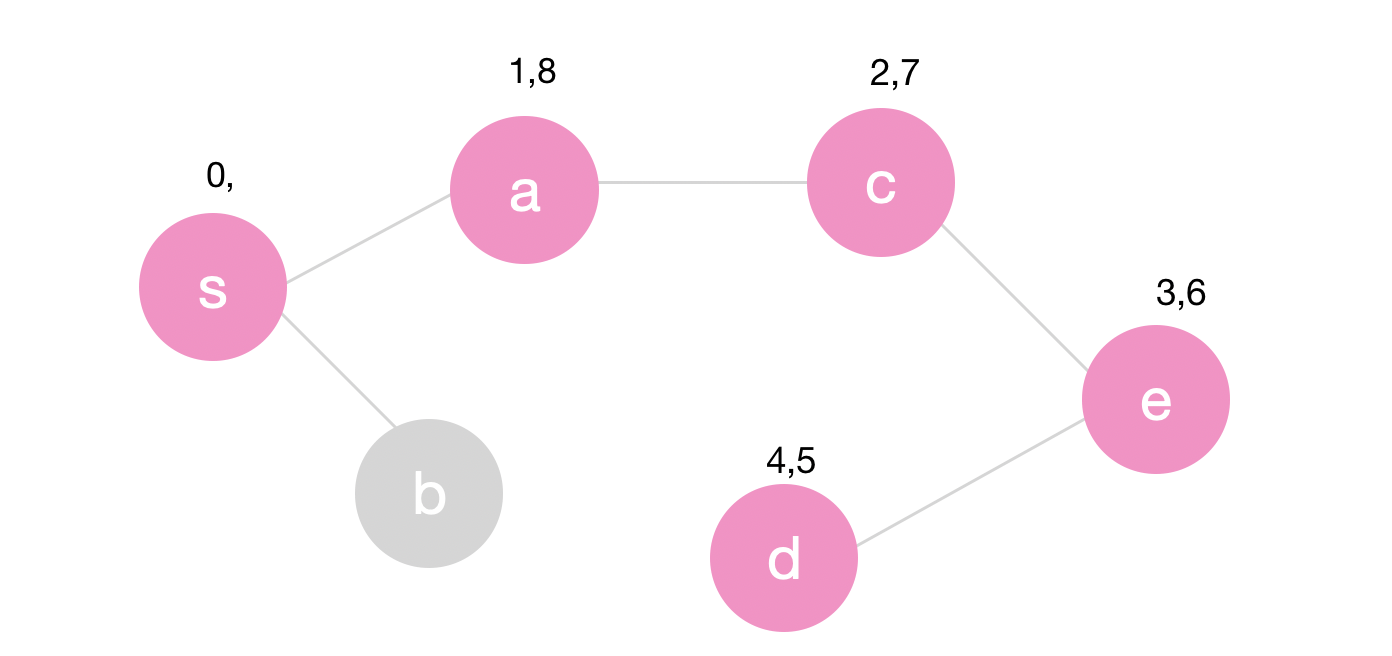
At this point, there will be no more vertices to traverse and so node \(d\) is now finished with time 5, followed by \(e\), \(c\) and then \(a\).
Finally, we will traverse node \(b\) with start time 9 and finish time 10. Node \(s\) will now be done with finish time \(11\).
Implementation
int dfs(int v, int current_time,
std::vector<std::vector<int>>& graph,
std::vector<std::pair<int,int>> ×,
std::vector<int> &visited) {
times[v].first = current_time++; // seeing v for the first time
visited[0] = true;
for (int i = 0; i < graph[v].size(); i++) {
int u = graph[v][i];
if (visited[u] == false) {
current_time = dfs(u, current_time, graph, times, visited);
current_time++;
}
}
times[v].second = current_time; // v is done bye forever
return current_time;
}Running Time
Similar to the analysis of breadth first search. We visit each vertex once only. That’s \(O(V)\) time. Therefore, we also visit the adjacency list of each vertex at most once and that’s \(O(E)\) time. Therefore, the total time is \(O(V+E)\).