Let $G=(V,E)$ be undirected, weighted graph with $V$ vertices and $E$ edges. A minimum spanning tree is a tree that connects all the vertices in $V$ of minimal cost. Kruskal’s algorithm is a greedy algorithm. We always take the cheapest edge from the graph that won’t create a cycle. In other words, Kruskal is maintaining a bunch of forests at each step. We slowly combine these trees to form the final single tree that covers all vertices.

Algorithm (slow version)

The simplest way to implement Kruskal is to sort the edges according to their weights in $O(E\log(E))$ time and then loop through the edges to pick the cheapest ones that don’t create a cycle. We can check for cycles in $O(E+V)$. So this algorithm ends up being really slow.

E = Sort the edges by non-decreasing weight.
MST = {}
for e in sorted E {
    if we can add e to MST without creating a cycle { // O(E+V)
        add e to MST
    }
}
return MST

Algorithm (fast version)

There is a much better way to implement Kruskal and boost its run time than the above method. The key to the faster version is using a special data structure call union-find. Union-find supports the following operations,

makeSet(u): creates a set $\{u\}$
find(u): returns the set that $u$ is in.
union(u,v): merge the set that $u$ is in with the set that $v$ is in.

How do we use union-find to boost the performance of Kruskal? We initialize $V$ sets for each of the vertices. We then loop through the sorted edges and union the two vertices only if they’re not in the same set already. This way we don’t need to check for cycles anymore.

E = Sort the edges by non-decreasing weight.
MST = {}
for v in V {
    makeSet(v)
}
for (u,v) in E {
    if find(u) != find(v) {
        add {u,v} to MST
        union(u,v)
    }
}
return MST

Example

In the above graph, we initialize the following forests $\{a\}, \{b\}, \{c\}, \{d\}, \{e\}, \{f\}$. We also sort the edges by non-decreasing weight and proceed to merge our forests. Assume the sorted order is the following: $\{a,b\}, \{b,f\}, \{a,f\}, \{e,d\}, \{c,e\}, \{b,c\}, \{c,f\}, \{f,e\}, \{c,d\}$

Iteration 0
The first edge to consider is $\{a,b\}$. Since $a$ and $b$ are not in the same set, we add the edge to the MST and combine both $a$ and $b$.

Iteration 1
We next consider $\{b,f\}$. Since $b$ and $f$ are not in the same set, we add the edge to the MST and combine both $b$ and $f$. So now we have the following forests: $\{a, b, f\}, \{c\}, \{d\}, \{e\}$

Iteration 2
We next consider $\{a,f\}$. Since $a$ and $f$ are in the same set, we skip this edge.

Iteration 3
We next consider $\{e,d\}$. Since $e$ and $d$ are not in the same set, we merge these two forests into one. We now have the following forests: $\{a, b, f\}, \{c\}, \{d, e\}$

$$ At the end of the algorithm, the minimum spanning tree is the following tree:

Proof of Correctness (Preliminarily)

Why does this algorithm find a minimum spanning tree? Before we can answer that, let’s define some terms and prove a lemma that will be useful in the main proof. Let $G=(V,E)$ be the graph below and let $S$ be the set of yellow edges in $G$.

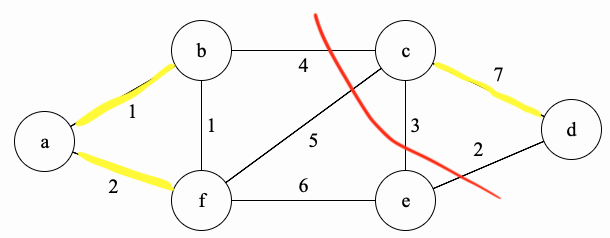
my photo

A cut is a partition of the vertices into two non-empty parts. the red line (cut) partitions $G$ into $\{a,b,f,e\}$ and $\{c,d\}$.
A cut respects $S$ if no edges in $S$ cross the cut. None of the yellow edges cross the red cut.
An edge crossing the cut is called light if it has the smallest weight of any edge crossing the cut. In this case, $\{e,d\}$ is a light edge.

Lemma: Let $S$ be a set of edges and consider a cut that respects $S$. Suppose there is an MST containing $S$. Let $\{u,v\}$ be a light edge. Then there is an MST containing $S \cup \{u,v\}$

Proof: Let $S$ be a set of edges and and consider a cut that respects $S$. Let $T$ be an MST containing $S$. Let $\{u,v\}$ be a light edge. There are two cases.
Case 1: $\{u,v\}$ is in $T$, then we’re done.
Case 2: $\{u,v\}$ is not in $T$. By the definition of MST, adding $\{u,v\}$ will create a cycle in $T$. Since the sets resulting from the cut must be non-empty. This means that we must have an edge that crosses the cut in $T$. Let that edge be $\{x,y\}$. Consider replacing $\{u,v\}$ with $\{x,y\}$ to produce the new tree $T'$. $T$ is still an MST since we deleted $\{x,y\}$. $T'$ has also a cost of at most the cost of $T$ since {u,v} is a light edge. Therefore, $T'$ is an MST which includes both $\{u,v\}$ and $S$ which is what we wanted to show. $\blacksquare$

Kruska's Proof of Correctness

Theorem: Kruskal will correctly find a minimum spanning tree

Proof:
Inductive Hypothesis: After adding the $t$‘th edge, there exists an MST with the edges added so far.

Base Case: After adding the 0’th edge, there exists an MST with the edges added so far.

Inductive Step: Suppose the inductive hypothesis holds for $t$. Let $S$ be the set containing the edges added so far and so there is an MST extending them by the inductive hypothesis. Kruskal adds the next edge that combines some trees $T_1$ and $T_2$ from $S$. Consider the cut $T_1$ and $V-T_1$. This cut respects $S$. By the Lemma above, that edge is safe to add. Therefore, there is still an MST extending the new set of edges.

Conclusion: After adding the $n-1$‘st edge, there exists an MST with the edges added so far. At this point we have reached all vertices and the $n-1$ edges we have is an MST.$\blacksquare$

Running Time

Assume we have $n$ vertices and $m$ edges. First of all, sorting the edges will take time $O(m\log(m)) = m\log(n^2) = O(m\log(n))$. If radixSort can be utilized then we can do this step in time $O(m)$.

We then have $n$ calls to makeSet, $2m$ calls to find and $n$ calls to union. These operations run in amortized time $O(\alpha(n))$ where $\alpha(n)$ is the inverse Ackerman function and $\alpha(n) \leq 4$ provided that $n$ is smaller than the number of atoms in the universe.

Therefore, the total time is just $O(m\log(n))$ which is similar to Prim if we use a Red Black Tree and closer to $O(m)$ if we use radixSort.

Implementation

Source Code

References

CS161 @ Stanford (With Mary Wootters)
CLRS