Suppose we have two line segments in two dimensions. Each line segment is determined by two given points. How can we determine if the two line segments intersect? Before answering this question, let’s review some concepts.

What is a line segment?

Given two points $p_1$ and $p_2$. A line segment $\overline{p_1p_2}$ is the set of convex combinations of $p_1$ and $p_2$. That is for any point $p_3$ on the line segment $\overline{p_1p_2}$, we have

$$ \begin{align*} x_{p_3} = \alpha x_{p_1} + (1-\alpha)x_{p_2} \\ y_{p_3} = \alpha y_{p_1} + (1-\alpha)y_{p_2} \end{align*} $$

where $0 \leq \alpha \leq 1$. $p_1$ and $p_2$ are the end points of the line segment.

Straddling

The algorithm CLRS presents is based on the idea of checking whether each line segment straddles the line containing the other line segment. 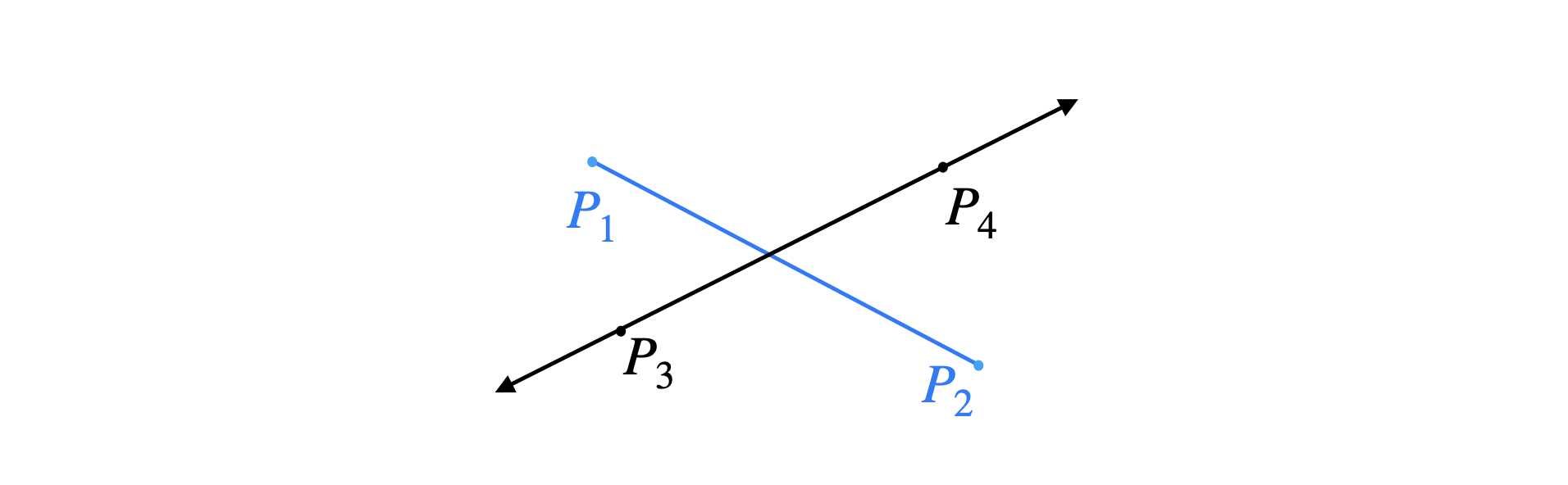In the above figure, consider the line segment $\overline{p_1p_2}$ and the line containing the segment $\overline{p_3p_4}$. We say that $\overline{p_1p_2}$ straddles the line containing $\overline{p_3p_4}$ if $p_1$ and $p_2$ are on opposite sides of the line. Should this check be enough to guarantee the intersection of both segments? No. Consider the following figure, 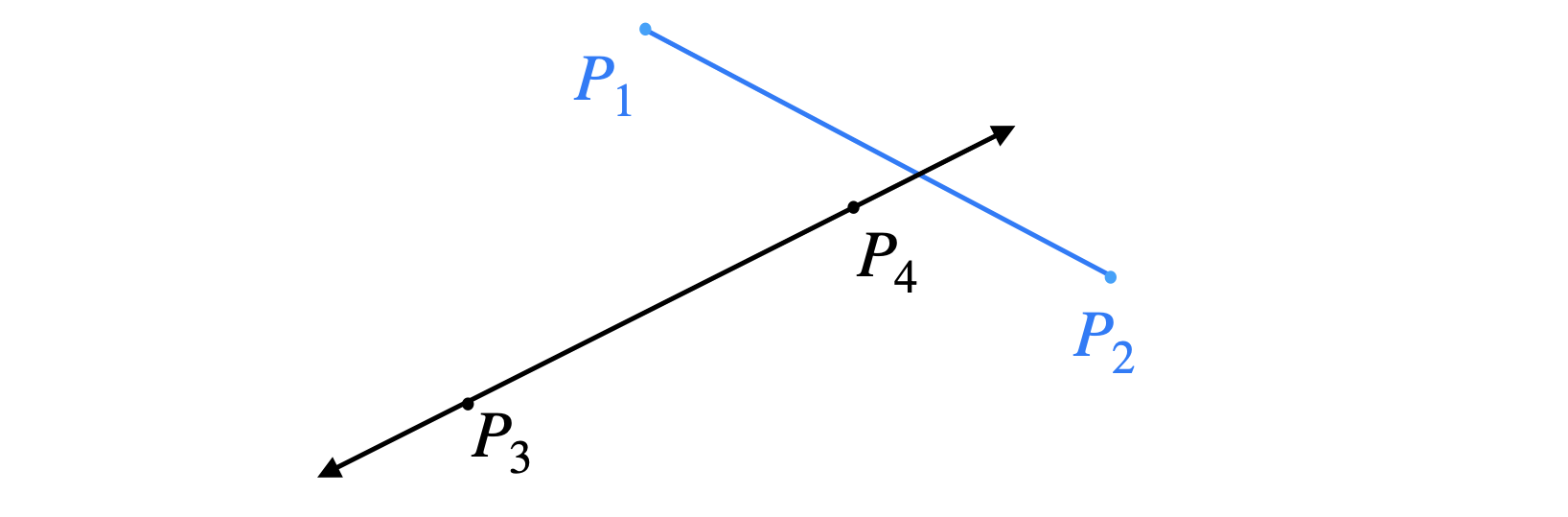In this case, segment $\overline{p_1p_2}$ straddles the line but it does intersect the segment $\overline{p_4p_3}$. We could fix this by also checking whether $\overline{p_3p_4}$ straddles the line containing $\overline{p_1p_2}$. Should this be enough now to handle everything? Unfortunately, we are still missing a case. Consider the following, 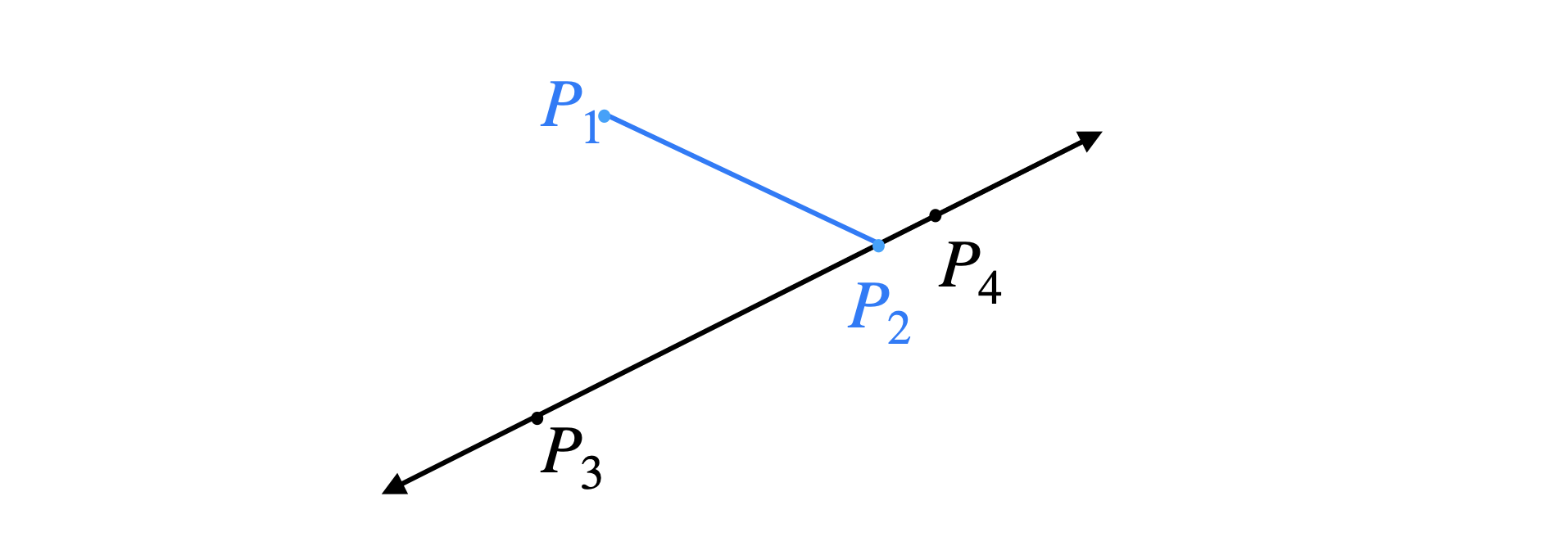In this case, one of the end points is on the line and so we’re not exactly on opposite sides of the line. Therefore, we need to check whether $p_1$ or $p_2$ falls on the line segment $\overline{p_4p_3}$.

Pseudocode

// line 1 = p1,p2 and line 2 = p3,p4
segment_intersection(p1,p2,p3,p4) {
    // first check whether each segment straddles the line
    // containing the other segment
    if (is_segment_straddling_line(p1,p2,p3,p4) &&
        is_segment_straddling_line(p3,p4,p1,p2)) {
        return true;
     }
    // otherwise check the boundary conditions
    // on_line_segment(px, py, pz) determines if px is 
    // on the line segment pypz
    if (on_line_segment(p1, p3, p4) || 
        on_line_segment(p2, p3, p4) || 
        on_line_segment(p3, p1, p2) || 
        on_line_segment(p4, p1, p2)) {
            return true;
    }
    return false;
}

The next questions would be how to check whether a line segment is straddling a line and how to check whether a point falls on a line segment. Both of these questions can be answered utilizing cross product.

Cross Product

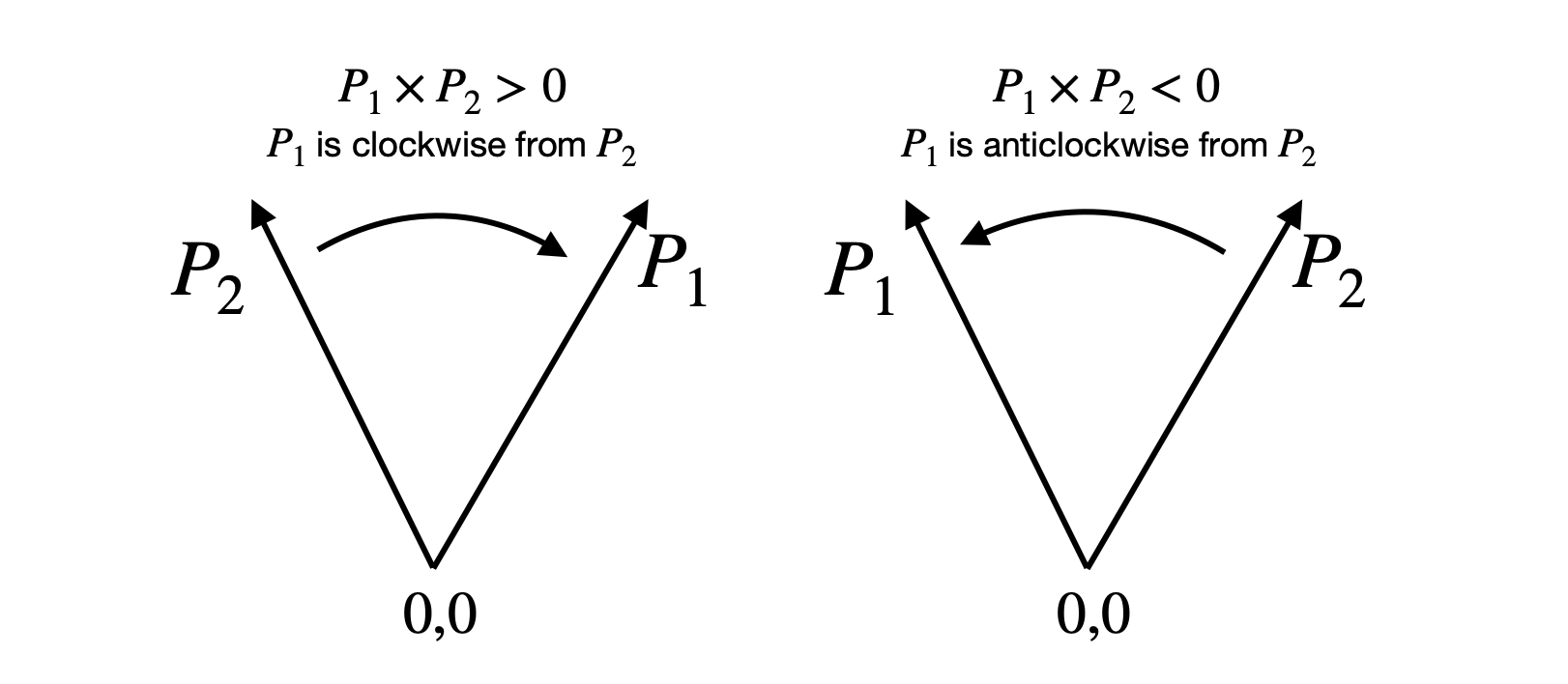Given two vectors $\vec{p_1}$ and $\vec{p_2}$. If the cross product $\vec{p_1} \times \vec{p_2}$ is positive, then we say that $\vec{p_1}$ is clockwise from/relative to $\vec{p_2}$ and we turn right at $p_2$. Similarly, if the cross product is negative then we say that $\vec{p_1}$ is anti-clockwise from/relative to $\vec{p_2}$ and we turn left at $p_2$.

Proof

(This is also exercise $33.1-1$)
If the cross product is positive then we know that $x_1y_2 - x_2y_1 > 0$.

$$ \begin{align*} x_1y_2 - x_2y_1 > 0 \\ x_1y_2 > x_2y_1 \\ \frac{y_2}{x_2} > \frac{y_1}{x_1} \end{align*} $$

Consider now the angle that both vectors make with the positive $x$ axis. In the below figure, 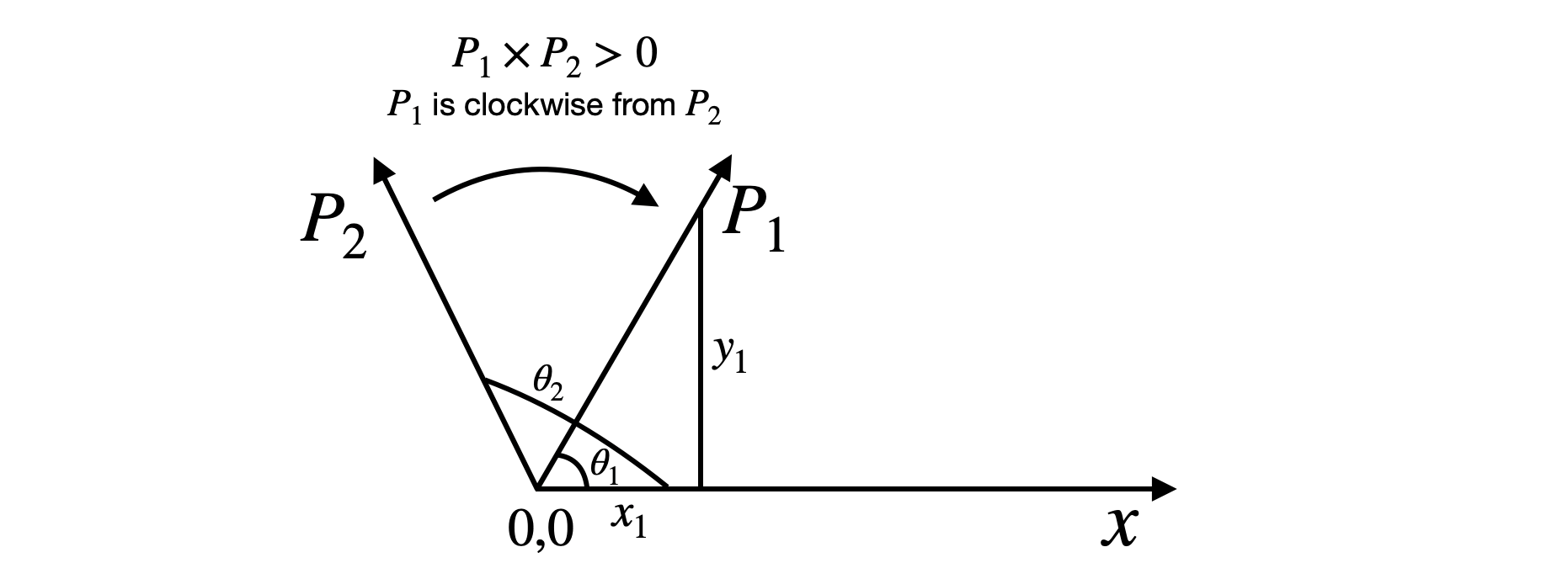we see that this angle is given by $\tan^{-1}{y/x}$. We also know that $\arctan$ is monotone and so since $\frac{y_2}{x_2} > \frac{y_1}{x_1}$ then we must have $\theta_2 > \theta_1$. Therefore, $p_1$ must be clockwise relative to $p_2$. Similarly, when the cross product is negative, we will see that $\frac{y_1}{x_1} > \frac{y_2}{x_2}$ and so $p_2$ must be anti-clockwise relative to $p_1$. (Ref (2)).

Checking whether a segment is straddling a line

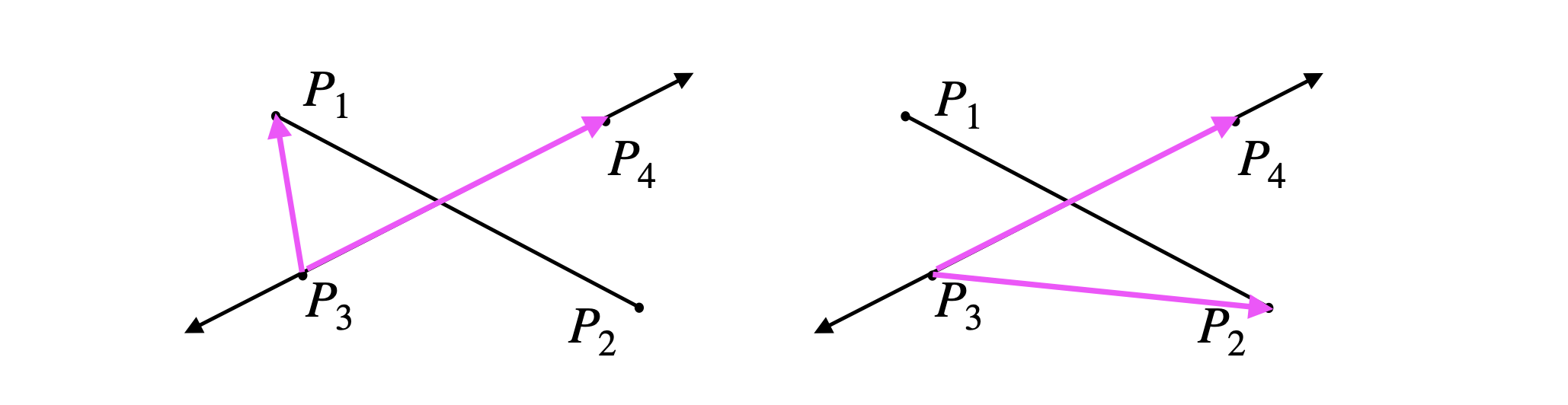Using the above idea, it becomes straight forward to determine whether a segment is straddling a line. Suppose we’re determining if segment $\overline{p_1p_2}$ is straddling the line containing $\overline{p_3p_4}$. We first find the result of the cross product $(p_1-p_3) \times (p_4-p_3)$. This will tell us whether $\vec{p_1-p_3}$ is clockwise or anti-clockwise relative to $\vec{p_4-p_3}$ (left figure). Next, we find $(p_2-p_3) \times (p_4-p_3)$ to determine if $\vec{p_2-p_3}$ is clockwise or anti-clockwise relative to $\vec{p_4-p_3}$ (right figure). Finally, we check if the products have different signs to rule out that $p_1$ and $p_2$ are on different sides of the line.

Checking whether a point falls on a line segment

Suppose we’re determining if point $p_1$ falls on the segment $\overline{p_3p_4}$. We first need to determine if all three points $p_1, p_3$ and $p_4$ are colinear. To do so, we can check the cross product we’ve computed previously, namely, $(p_1-p_3) \times (p_4-p_3)$. If this product is 0, then we know that the three points are colinear.

Next, we need to determine if the point $p_1$ falls between the segment $\overline{p_3p_4}$ or on one of its end points. To do so, we need to check that the x-coordinate of $p_1$ falls in the range of $min(x_3,x_4), max(x_3,x_4)$ and the y-coordinate falls in the range $min(y_3,y_4),max(y_3,y_4)$.