 Given an array \(A\) and two indices \(i \leq j\) that are not known in advance. The RMQ problem solves the problem of finding the minimum element in the range \(A[i],A[i+1],...,A[j-1],A[j]\).
Given an array \(A\) and two indices \(i \leq j\) that are not known in advance. The RMQ problem solves the problem of finding the minimum element in the range \(A[i],A[i+1],...,A[j-1],A[j]\).
Definitions
Let \(\langle p(n), q(n)\rangle\) be the complexity of an algorithm with preprocessing time \(p(n)\) and query time \(q(n)\).
Algorithm 1: no preprocessing
The simplest approach is to not do any kind of preprocessing on the input and just compute the minimum for each query. Therefore, we will have \(\langle p(n), q(n)\rangle = \langle O(1), O(n)\rangle\).
Algorithm 2: precompute all ranges
We compute the minimum element for all possible ranges. There are \(O(n^2)\) possible ranges. We need $O(n)$ time to compute the minimum in each range so the total time preprocessing time is \(p(n) = O(n^3)\) and therefore, we have \(\langle p(n), q(n)\rangle = \langle O(n^3), O(1)\rangle\).
Algorithm 3: precompute all ranges with dynamic programming
We can use dynamic programming to compute all the ranges. Given that we know the minimum \(m\) to a range \(A[i,...j]\), the solution to the range \(A[i,...j+1]\) is just \(min(m, A[j+1])\).
int dp[n][n], a[n]={...}
// given the minimum to range dp[i,j-1],
// the minimum to range [i,j+1] = min(dp[i,j-1],a[j])
for (int i = 0; i < n; i++) {
dp[i][i] = a[i];
}
for (int i = 1; i < n; i++) {
for (int j = i+1; j < n; j++) {
// for range i..j
dp[i][j] = std::min(dp[i][j-1],a[j]);
}
}Therefore, \(p(n) = O(n^2)\) and we have \(\langle p(n), q(n)\rangle = \langle O(n^2), O(1)\rangle\).
Algorithm 4: block decomposition
 Approach:
Approach:
We can split the input into \(O(n/b)\) blocks of block size \(b\) and compute the minumum in each block.
Preprocessing Time:
We need to find the minimum for each block. Time to find the minimum for all blocks is \(p(n) = n/b*b = O(n)\).
Query Time:
Given indices \(i\) and \(j\).
(1) We find the minimum for the internal blocks between \(i\) and \(j\) in time \(O(n/b)\).
(2) We need to look at possibly all the elements in the two outer blocks. This can be done in time \(O(2b)=O(b)\).
Therefore, \(q(n) = O(b + (n/b))\):
What is the optimal block size?
We can take the derivative of \(b + n/b\) to find the value that minimizes \(b\). This value is \(b = \sqrt{n}\). Therefore, the query time is \(q(n) = O(b + (n/b)) = O(\sqrt{n} + (n/\sqrt{n})) = O(\sqrt{n})\).
Finally we will have \(\langle p(n), q(n)\rangle = \langle O(n), O(\sqrt{n})\rangle\).
// given that we computed each block's minimum
// given indices i and j, we can do something like this
int block_i = i/b;
int block_j = j/b;
int min = INT_MAX;
// search internal blocks
for (int k = block_i + 1; k < block_j; k++) {
if (min > block[k]) {
min = block[k];
}
}
// search elements in the outer blocks
int k = std::max(i, block_i*b);
int m = std::min(block_i*b+b, j);
for (; k <= m; k++) {
if (min > a[k]) {
min = a[k];
}
}
k = std::max(i, block_j*b);
m = std::min(block_j*b+b, j);
for (; k <= m; k++) {
if (min > a[k]) {
min = a[k];
}
}
printf("%d ", min);
Algorithm 5: sparse tables

Going back to the dynamic programmnig solution. Instead of computing all ranges, we can instead compute a specific set of ranges. How? For each index, we compute the minimum for the ranges
So for the array above we will have the following minimums:
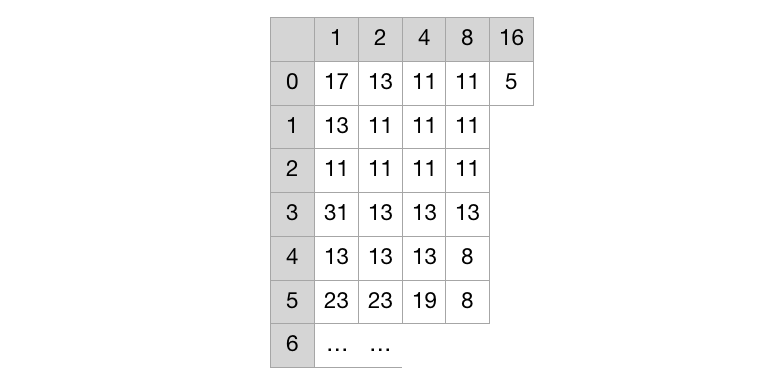
Each Entry, \(M[i,j]\) represents the minimum for the range \(\{i,i+2^j\}\). Since we’re computing \(n\log(n)\) ranges, therefore, this table has size \(O(nlogn)\). We can further use dynamic programmnig to fill this table out.
Dyanmic Programming
Notice that any region can be divided into two regions. The intuition is that since we’re computing the minimum for ranges that are powers of 2, then any region of size \(2^k\) can be divided into two regions of size \(2^{k-1}\) which we compute first. In the example below, we want to find the minimum for the gray range that starts at \(i\) and of size \(2^j\). To do so, we divide the range into the blue and yellow regions, each of size \(2^{j-1}\). The blue region is just \(M[i,j-1]\) and the yellow region is just \(M[i+2^{j-1},j-1]\)

Therefore, the recursive formula to compute \(M[i,j]\) is:
We can use something similar to this to compute the values based on the recurrence above
void preprocess_sparse(int *a, int n, int M[MAX][LOGMAX]) { // O(nlog(n))
// 2^0
for (int i = 0; i < n; i++) {
M[i][0] = a[i];
}
int lg = log2(n);
// for each power of 2
for (int j = 1; j <= lg; j++) {
// fill each row
for (int i = 0; i + (1 << j) - 1 < n; i++) {
M[i][j] = std::min(M[i][j-1], M[i+(1<<(j-1))][j-1]);
}
}
}Preprocessing Time:
Notice that for each index, we’re computing \(\log{n}\) ranges. Therefore, the total preprocessing time \(p(n) = O(n\log(n))\).
Query Time:
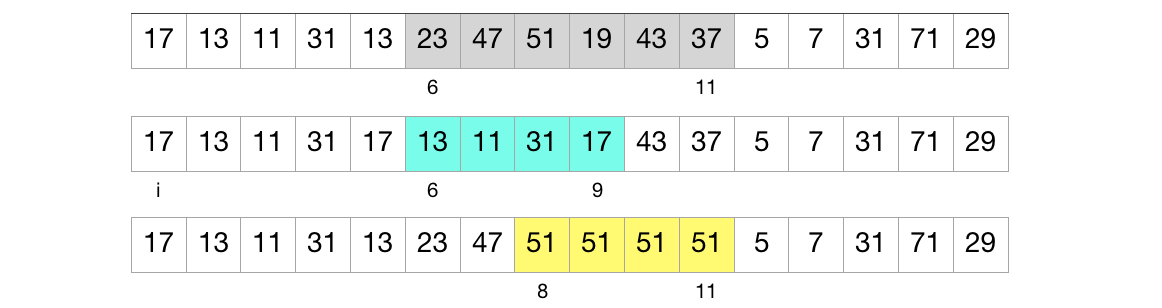
Given indices \(i\) and \(j\):
(1) We know the number of elements in the range \(\{i,j\}\) is \(j-i+1\). We can then find the largest block of size \(2^k\) that fits in that range. We can simply take the log of \(j - i + 1\) to get \(k\). This is done in \(O(1)\) time.
(2) We can now divide the range into two possibly overlapping regions, \(\{i, i+2^k-1\}\) which is \(M[i][k]\) and \(\{j-2^k+1, j\}\) which is \(M[j-2^k+1][k]\). We can return the minimum of the two ranges. The total time is therefore \(O(1)\).
This code just tests all possible ranges:
void test_sparse(int *a, int n) {
int M[MAX][LOGMAX];
preprocess_sparse(a, n, M);
// query time
for (int i = 0; i < n; i++) {
for (int j = 0; j < i; j++) {
printf("\t");
}
for (int j = i; j < n; j++) {
// given indices i and j
int k = log2(j-i+1);
printf("%d\t", std::min(M[i][k], M[j-(1<<k)+1][k]));
}
printf("\n");
}
}
Finally we will have \(\langle p(n), q(n)\rangle = \langle O(n\log(n)), O(1)\rangle\).
Implementation
https://github.com/strncat/algorithms-and-data-structures/blob/master/rmq/rmq.cpp
References
- CS166 Lecture Slides http://web.stanford.edu/class/cs166/lectures/00/Small00.pdf
- Fischer, Johannes and Heun, Volker. Theoretical and Practical Improvements on the RMQ-Problem, with Applications to LCA and LCE